题目内容
15.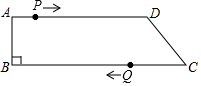 如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=30cm.点P从点A出发,以1cm/s的速度向点D移动,点Q从点C出发,以3cm/s的速度向点B运动,点P和点Q分别从点A和点C同时出发,移动时间为ts.规定若其中一个动点先到达端点(终点)时,另一个动点也随之停止运动.
如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=30cm.点P从点A出发,以1cm/s的速度向点D移动,点Q从点C出发,以3cm/s的速度向点B运动,点P和点Q分别从点A和点C同时出发,移动时间为ts.规定若其中一个动点先到达端点(终点)时,另一个动点也随之停止运动.(1)求时间t的取值范围;
(2)当四边形ABQP为矩形时,求时间t的值;
(3)是否存在时间t的值,使得△APQ的面积是△ABC的面积的一半?若存在,请求出t的值,若不存在,说明理由.
分析 (1)根据运动速度是距离即可得出结论;
(2)有矩形的性质得出AP=BQ,建立方程求解即可得出结论;
(3)假设△APQ的面积是△ABC的面积的一半,求出时间,判断是否在0≤t≤10内,即可得出结论.
解答 解:(1)点P停止的时间是24÷1=24s,点Q停止的时间是30÷3=10s,
所以时间t的取值范围是0≤t≤10.
(2)由运动知,AP=t,CQ=3t,
∴BQ=30-3t,
若四边形ABQP是矩形.
∴AP=BQ.
即t=30-3t.
∴t=7.5.
(3)不存在.理由如下:
若△APQ的面积是△ABC的面积的一半时,
∴$\frac{1}{2}$AP×AB=$\frac{1}{2}×\frac{1}{2}$×AB×BC.
∴t=$\frac{1}{2}$×30=15.
∵t的取值范围是0≤t≤10.
∴不存在t的值,使得使得△APQ的面积是△ABC的面积的一半.
点评 此题是四边形综合题,主要考查了梯形的性质,矩形的性质,三角形的面积公式,解本题的关键是用方程的思想解决问题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
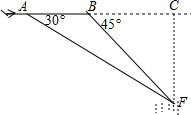 “马航事件”的发生引起了我国政府的高度重视,我国政府迅速派出了舰船和飞机到相关海域进行搜寻.如图,在一次空中搜寻中,水平飞行的飞机在点A处测得前方海面的点F处有疑似飞机残骸的物体(该物体视为静止).此时的俯角为30°,为了便于观察,飞机继续向前飞行了800米到达B点,此时测得点F点俯角为45°.请你计算当飞机飞临F点的正上方点C时(点A、B、C在同一直线上),竖直高度CF约为多少米?(结果保留整数,参考数值:$\sqrt{3}$≈1.7)
“马航事件”的发生引起了我国政府的高度重视,我国政府迅速派出了舰船和飞机到相关海域进行搜寻.如图,在一次空中搜寻中,水平飞行的飞机在点A处测得前方海面的点F处有疑似飞机残骸的物体(该物体视为静止).此时的俯角为30°,为了便于观察,飞机继续向前飞行了800米到达B点,此时测得点F点俯角为45°.请你计算当飞机飞临F点的正上方点C时(点A、B、C在同一直线上),竖直高度CF约为多少米?(结果保留整数,参考数值:$\sqrt{3}$≈1.7)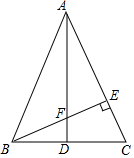 如图,△ABC中,AB=AC,AD是∠BAC的平分线,交BC于D,过点B作BE⊥AC于E,交AD于F,又知AF=2BD,△BCE与△AFE全等吗?为什么?
如图,△ABC中,AB=AC,AD是∠BAC的平分线,交BC于D,过点B作BE⊥AC于E,交AD于F,又知AF=2BD,△BCE与△AFE全等吗?为什么?
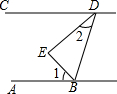 如图所示,BE是∠ABD的平分线,DE是∠BDC的平分线,且∠1+∠2=90°,那么直线AB、CD的位置关系如何?并说明理由.
如图所示,BE是∠ABD的平分线,DE是∠BDC的平分线,且∠1+∠2=90°,那么直线AB、CD的位置关系如何?并说明理由.