题目内容
18.解下列不等式(组),并把解集在数轴上表示出来:(1)$\left\{\begin{array}{l}{2x+6>0}\\{1-2x≥0}\end{array}\right.$
(2)1-$\frac{x+6}{2}$<$\frac{2x+1}{3}$.
分析 (1)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
(2)根据解一元一次不等式基本步骤:去分母、去括号、移项、合并同类项、系数化为1可得.
解答 解:(1)$\left\{\begin{array}{l}{2x+6>0}&{①}\\{1-2x≥0}&{②}\end{array}\right.$,
由①,解得x>-3,
由②,解得:x≤$\frac{1}{2}$,
∴原不等式组的解集为-3<x≤$\frac{1}{2}$.
(2)去分母,6-3(x+6)<2(2x+1),
去括号,得:6-3x-18<4x+2,
移项、合并,得:-7x<14,
系数化为1,得:x>-2,
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.运行程序如图所示,规定:从“输入一个值x”到“结果是否>95”为一次程序操作,如果程序操作进行了两次才停止,那么x的取值范围是( )


| A. | x>23 | B. | 23<x≤47 | C. | 11≤x<23 | D. | x≤47 |
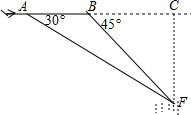 “马航事件”的发生引起了我国政府的高度重视,我国政府迅速派出了舰船和飞机到相关海域进行搜寻.如图,在一次空中搜寻中,水平飞行的飞机在点A处测得前方海面的点F处有疑似飞机残骸的物体(该物体视为静止).此时的俯角为30°,为了便于观察,飞机继续向前飞行了800米到达B点,此时测得点F点俯角为45°.请你计算当飞机飞临F点的正上方点C时(点A、B、C在同一直线上),竖直高度CF约为多少米?(结果保留整数,参考数值:$\sqrt{3}$≈1.7)
“马航事件”的发生引起了我国政府的高度重视,我国政府迅速派出了舰船和飞机到相关海域进行搜寻.如图,在一次空中搜寻中,水平飞行的飞机在点A处测得前方海面的点F处有疑似飞机残骸的物体(该物体视为静止).此时的俯角为30°,为了便于观察,飞机继续向前飞行了800米到达B点,此时测得点F点俯角为45°.请你计算当飞机飞临F点的正上方点C时(点A、B、C在同一直线上),竖直高度CF约为多少米?(结果保留整数,参考数值:$\sqrt{3}$≈1.7)