题目内容
2. 在△ABC中,∠B和∠C的平分线交于点O.
在△ABC中,∠B和∠C的平分线交于点O.(1)求证:点O在∠A的平分线上;
(2)求∠BOC与∠A的关系式.
分析 (1)作OD⊥BC于D,OE⊥AC于E,OF⊥BA于F,根据角平分线的性质证明OE=OF,根据角平分线的判定定理证明结论;
(2)根据角平分线的定义和三角形内角和定理进行计算即可.
解答 (1)证明: 作OD⊥BC于D,OE⊥AC于E,OF⊥BA于F,
作OD⊥BC于D,OE⊥AC于E,OF⊥BA于F,
∵BO平分∠ABC,OD⊥BC,OF⊥BA,
∴OF=OD,
同理,OD=OE,
∴OE=OF,OE⊥AC,OF⊥BA,
∴点O在∠A的平分线上;
(2)∵BO平分∠ABC,
∴∠OBC=$\frac{1}{2}$∠ABC,
同理∠OCB=$\frac{1}{2}$∠ACB,
∴∠BOC=180°-$\frac{1}{2}$(∠ABC+∠ACB)
=180°-$\frac{1}{2}$(180°-∠A)
=90°+$\frac{1}{2}$∠A.
点评 本题考查的是角平分线的定义和性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
12.多项式2-3x2y+2y2-x的项数与次数分别是( )
| A. | 4,6 | B. | 4,3 | C. | 3,4 | D. | 3,3 |
 张亮学习小组调查了某工厂部分工人的月收入情况,绘制出如图所示的扇形统计图,求这部分工人月收入的众数与平均数.
张亮学习小组调查了某工厂部分工人的月收入情况,绘制出如图所示的扇形统计图,求这部分工人月收入的众数与平均数.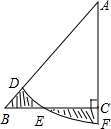 如图,在Rt△ABC中,AC=BC,以A为圆心作$\widehat{DF}$,交AB于点D,交AC的延长线于点F,交BC于点E.若图中两个阴影部分的面积相等,求AC与AF的长度之比(π取3).
如图,在Rt△ABC中,AC=BC,以A为圆心作$\widehat{DF}$,交AB于点D,交AC的延长线于点F,交BC于点E.若图中两个阴影部分的面积相等,求AC与AF的长度之比(π取3).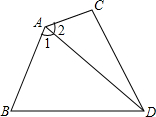 如图,AB=2AC,∠1=∠2、DA=DB,求证:DC⊥AC.
如图,AB=2AC,∠1=∠2、DA=DB,求证:DC⊥AC.