题目内容
19.已知a2+b2-4a-2b+5=0,求$\frac{\sqrt{a}+b}{\sqrt{3b}-\sqrt{a}}$的值.分析 已知等式左边变形后,利用非负数的性质求出a与b的值,即可确定出所求式子的值.
解答 解:∵a2+b2-4a-2b+5=(a-2)2+(b-1)2=0,
∴a-2=0,b-1=0,
∴a=2,b=1,
则$\frac{\sqrt{a}+b}{\sqrt{3b}-\sqrt{a}}$=$\frac{\sqrt{2}+1}{\sqrt{3}-\sqrt{2}}$=($\sqrt{2}$+1)($\sqrt{3}$+$\sqrt{2}$)=$\sqrt{6}$+2+$\sqrt{3}$+$\sqrt{2}$.
点评 此题考查了配方法的应用,以及非负数的性质,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
9.如果2是方程c-x2=0的一个根,那么常数c是( )
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
8.下列各图中,∠1与∠2互为余角的是( )
| A. |  | B. |  | C. |  | D. |  |
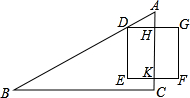 如图,正方形城邑DEFG的四面正中各有城门,出北门20步的A处(HA=20步)有一树木,由南门14步到C处(KC=14步),再向西行1775步到B处(CB=1775步),正好看到A处的树木(点D在直线AB上),则城邑的边长为250步.
如图,正方形城邑DEFG的四面正中各有城门,出北门20步的A处(HA=20步)有一树木,由南门14步到C处(KC=14步),再向西行1775步到B处(CB=1775步),正好看到A处的树木(点D在直线AB上),则城邑的边长为250步.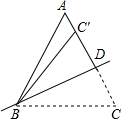 如图,在△ABC中,AB=AC=10,将△ABC沿直线BD翻折,使点C落在AC边上的点C′处,若AC′=2,则折痕BD的长8.
如图,在△ABC中,AB=AC=10,将△ABC沿直线BD翻折,使点C落在AC边上的点C′处,若AC′=2,则折痕BD的长8.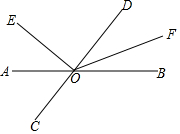 如图,直线AB,CD相交于点O,OE⊥CD,OF平分∠BOD.
如图,直线AB,CD相交于点O,OE⊥CD,OF平分∠BOD.