题目内容
11.有三张正面分别标有数字0,1,-3的卡片,它们除了数字不同外其余全部相同,现将它们背面朝上,洗匀后从中抽出一张记下数字,放回洗匀后在从中随机抽出一张记下数字.(1)请用列表或画树状图的方法,表示两次抽出卡片上的数字的所有结果;
(2)将第一次抽出的数字作为点的横坐标x,第二次抽出的数字作为点的纵坐标y,求点(x,y)落在抛物线y=x2+2x-3上的概率.
分析 (1)根据题意画出树状图即可得;
(2)结合树状图,利用概率公式计算即可.
解答 解:(1)画树状图如下:
(2)在所有9种等可能结果中,落在抛物线y=x2+2x-3上的有(0,-3)、(1,-2)、(-2,0)这3种结果,
∴点(x,y)落在抛物线y=x2+2x-3上的概率为$\frac{3}{9}$=$\frac{1}{3}$.
点评 此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
6.(1)图(1)是正方体木块,把它切去一块,可能得到形如图(2),(3),(4),(5)的木块.

我们知道,图(1)的正方体木块有8个顶点,12条棱,6个面,请你将图(2),(3),(4),(5)中木块的顶点数,棱数,面数填入表:
(2)观察表,请你归纳上述各种木块的顶点数,棱数,面数之间的数量关系,这种数量关系是:
顶点数+面数-2=棱数.
(3)图⑥是用虚线画出的正方体木块,请你想象一种与图②~⑤不同的切法,把切去一块后得到的那一块的每条棱都改画成实线,则该木块的顶点数为8,棱数为12,面数为6.这与你(2)题中所归纳的关系是否相符?


我们知道,图(1)的正方体木块有8个顶点,12条棱,6个面,请你将图(2),(3),(4),(5)中木块的顶点数,棱数,面数填入表:
| 图 | 顶点数 | 棱数 | 面数 |
| (1) | 8 | 12 | 6 |
| (2) | 6 | 9 | 5 |
| (3) | 8 | 12 | 6 |
| (4) | 8 | 13 | 7 |
| (5) | 10 | 15 | 7 |
顶点数+面数-2=棱数.
(3)图⑥是用虚线画出的正方体木块,请你想象一种与图②~⑤不同的切法,把切去一块后得到的那一块的每条棱都改画成实线,则该木块的顶点数为8,棱数为12,面数为6.这与你(2)题中所归纳的关系是否相符?

3.下列图形中不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
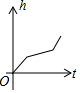
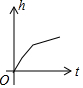
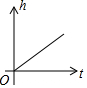
 有一容器的形状如图所示,现匀速地向该容器内注水,直到把容器注满,在注水过程中,容器内的水面高度h与注水时间t的大致图象为( )
有一容器的形状如图所示,现匀速地向该容器内注水,直到把容器注满,在注水过程中,容器内的水面高度h与注水时间t的大致图象为( )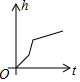
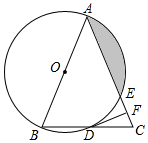 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC;垂足为点F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC;垂足为点F.