题目内容
4.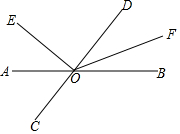 如图,直线AB,CD相交于点O,OE⊥CD,OF平分∠BOD.
如图,直线AB,CD相交于点O,OE⊥CD,OF平分∠BOD.(1)图中除直角外,请写出一对相等的角:∠DOB=∠AOC,∠AOD=∠BOC(写出符合的一对即可);
(2)若∠AOE=28°,求∠BOD和∠COF的度数.
分析 (1)根据对顶角相等可得∠DOB=∠AOC,∠AOD=∠BOC;
(2)根据垂直定义可得∠COE=90°,进而可得∠AOC的度数,再由对顶角相等可得∠BOD的度数,由角平分线的性质可得∠DOF的度数,再根据邻补角互补可得∠COF的度数.
解答 解:(1)∠DOB=∠AOC,∠AOD=∠BOC;
故答案为:∠DOB=∠AOC,∠AOD=∠BOC;
(2)∵OE⊥CD,
∴∠COE=90°,
∵∠AOE=28°,
∴∠AOC=62°,
∵OF平分∠BOD,
∴∠DOF=$\frac{1}{2}$∠BOD=31°,
∴∠COF=180°-31°=149°.
点评 此题主要考查了对顶角,邻补角,以及垂直定义,关键是掌握对顶角相等,邻补角互补.

练习册系列答案
相关题目
14.下列图形中,是中心对称图形但不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若BE:BC=1:4,则S△BDE:S△ACD的比为1:12.
如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若BE:BC=1:4,则S△BDE:S△ACD的比为1:12.