题目内容
4.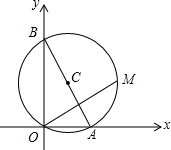 如图,已知A,B两点的坐标分别为(2$\sqrt{3}$,0),(0,10),M是△AOB外接圆⊙C上的一点,且∠AOM=30°,则点M的坐标为(4$\sqrt{3}$,4).
如图,已知A,B两点的坐标分别为(2$\sqrt{3}$,0),(0,10),M是△AOB外接圆⊙C上的一点,且∠AOM=30°,则点M的坐标为(4$\sqrt{3}$,4).
分析 由勾股定理求出AB的长,由圆周角定理得出AB为直径,求出半径和圆心C的坐标,过点C作CF∥OA,过点P作ME⊥OA于E交CF于F,作CN⊥OE于N,设ME=x,得出OE=$\sqrt{3}$x,在△CMF中,根据勾股定理得出方程,解方程即可.
解答 解:∵A,B两点的坐标分别为(2$\sqrt{3}$,0),(0,10),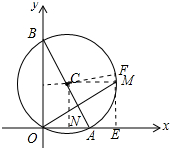
∴OB=10,OA=2$\sqrt{3}$,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=4$\sqrt{7}$,
∵∠AOB=90°,
∴AB是直径,CM=2$\sqrt{7}$,
∴Rt△AOB外接圆的圆心为AB中点,
∴C点坐标为($\sqrt{3}$,5),
过点C作CF∥OA,过点M作ME⊥OA于E交CF于F,作CN⊥OE于N,如图所示:
则ON=AN=$\frac{1}{2}$OA=$\sqrt{3}$,
设ME=x,
∵∠AOM=30°,
∴OE=$\sqrt{3}$x
∴∠CFM=90°,
∴MF=5-x,CF=$\sqrt{3}$x-$\sqrt{3}$,CM=2$\sqrt{7}$,
在△CMF中,根据勾股定理得:($\sqrt{3}$x-$\sqrt{3}$)2+(5-x)2=(2$\sqrt{7}$)2,
解得:x=4或x=0(舍去),
∴OE=$\sqrt{3}$x=4$\sqrt{3}$
故答案为:(4$\sqrt{3}$,4).
点评 本题考查的是圆周角定理、直角三角形的性质、勾股定理;熟练掌握圆周角定理,由勾股定理得出方程是解决问题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
15.下列计算中,不正确的是( )
| A. | (-2x2y)3=-6x6y3 | B. | -2x+3x=x | C. | 6xy2÷2xy=3y | D. | 2xy2•(-x)=-2x2y2 |
12.-1的绝对值是( )
| A. | -1 | B. | 1 | C. | 0 | D. | ±1 |
13.下列计算正确的是( )
| A. | 3a+2a2=5a3 | B. | -3a-2a=-5a | C. | 6a2÷2a2=3a2 | D. | 3a•2a=6a |
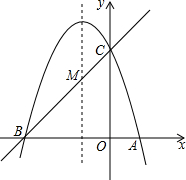 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.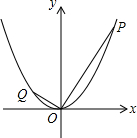 如图,已知点P是抛物线y=x2上的动点(点P在第一象限内),连结OP,过点O作OP的垂线交抛物线于另一点Q,当点P的横坐标是2时,点Q的坐标是(-$\frac{1}{2}$,$\frac{1}{4}$).
如图,已知点P是抛物线y=x2上的动点(点P在第一象限内),连结OP,过点O作OP的垂线交抛物线于另一点Q,当点P的横坐标是2时,点Q的坐标是(-$\frac{1}{2}$,$\frac{1}{4}$).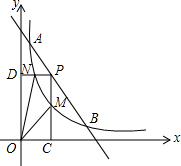 如图,一次函数与反比例函数的图象交于A(1,12)和B(6,2)两点.点P是线段AB上一动点(不与点A和B重合),过P点分别作x、y轴的垂线PC、PD交反比例函数图象于点M、N,则四边形PMON面积的最大值是$\frac{25}{2}$.
如图,一次函数与反比例函数的图象交于A(1,12)和B(6,2)两点.点P是线段AB上一动点(不与点A和B重合),过P点分别作x、y轴的垂线PC、PD交反比例函数图象于点M、N,则四边形PMON面积的最大值是$\frac{25}{2}$.