题目内容
16.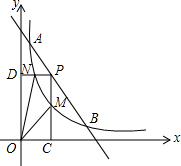 如图,一次函数与反比例函数的图象交于A(1,12)和B(6,2)两点.点P是线段AB上一动点(不与点A和B重合),过P点分别作x、y轴的垂线PC、PD交反比例函数图象于点M、N,则四边形PMON面积的最大值是$\frac{25}{2}$.
如图,一次函数与反比例函数的图象交于A(1,12)和B(6,2)两点.点P是线段AB上一动点(不与点A和B重合),过P点分别作x、y轴的垂线PC、PD交反比例函数图象于点M、N,则四边形PMON面积的最大值是$\frac{25}{2}$.
分析 由点A、B的坐标利用待定系数法即可求出一次函数与反比例函数的解析式,设出点P的坐标为(n,-2n+14)(1<n<6).由反比例的函数解析式表示出来M、N点的坐标,分割矩形OCPD,结合矩形和三角形的面积公式即可得出结论.
解答 解:设反比例函数解析式为y=$\frac{m}{x}$,一次函数解析式为y=kx+b,
由已知得:12=$\frac{m}{1}$和$\left\{\begin{array}{l}{12=k+b}\\{2=6k+b}\end{array}\right.$,
解得:m=12和$\left\{\begin{array}{l}{k=-2}\\{b=14}\end{array}\right.$.
∴一次函数解析式为y=-2x+14,反比例函数解析式为y=$\frac{12}{x}$.
∵点P在线段AB上,
∴设点P的坐标为(n,-2n+14)(1<n<6).
令x=n,则y=$\frac{12}{n}$;
令y=-2n+14,则$\frac{12}{x}$=-2n+14,解得:x=$\frac{6}{7-n}$.
∴点M(n,$\frac{12}{n}$),点N($\frac{6}{7-n}$,-2n+14).
S四边形PMON=S矩形OCPD-S△ODN-S△OCM=n(-2n+14)-$\frac{1}{2}$n•$\frac{12}{n}$-$\frac{1}{2}$•$\frac{6}{7-n}$•(-2n+14)=-2n2+14n-12=-2$(n-\frac{7}{2})^{2}$+$\frac{25}{2}$.
∴当n=$\frac{7}{2}$时,四边形PMON面积最大,最大面积为$\frac{25}{2}$.
故答案为:$\frac{25}{2}$.
点评 本题考查了反比例函数与一次函数的交点问题以及待定系数法求函数解析式,解题的关键是利用分割法求出四边形PMON面积关于点P横坐标的函数关系式.本题属于基础题,难度不大,解决该题型题目时,根据分割法找出面积的函数关系式,再结合函数的性质(单调性、二次函数的顶点之类)来解决最值问题.

 53随堂测系列答案
53随堂测系列答案| A. | $\frac{1}{2016}$ | B. | -$\frac{1}{2016}$ | C. | 2016 | D. | -2016 |
| A. | x3•x5=x15 | B. | x4÷x=x3 | C. | 3x2•4x2=12x2 | D. | (x5)2=x7 |
| 岗位 | 董事长 | 副董事长 | 董事 | 总经理 | 经理 | 部门A | 部门B | 部门C | 部门D | 部门E |
| 人数 | 1 | 1 | 3 | 1 | 4 | 5 | 12 | 20 | 2 | 1 |
| 月工资数(元) | 15000 | 12000 | 10000 | 9000 | 4000 | 2000 | 1800 | 1500 | 800 | 700 |
(2)求月工资的众数;工会主席用众数作为代表数,这是为什么?
(3)求月工资的中位数;税务工作人员用中位数作为代表数,这是为什么?
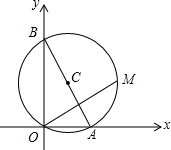 如图,已知A,B两点的坐标分别为(2$\sqrt{3}$,0),(0,10),M是△AOB外接圆⊙C上的一点,且∠AOM=30°,则点M的坐标为(4$\sqrt{3}$,4).
如图,已知A,B两点的坐标分别为(2$\sqrt{3}$,0),(0,10),M是△AOB外接圆⊙C上的一点,且∠AOM=30°,则点M的坐标为(4$\sqrt{3}$,4). 如图,反比例函数y=$\frac{k}{2x}$和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+k,b+k+2)两点且点A在第一象限,是两个函数的一个交点;
如图,反比例函数y=$\frac{k}{2x}$和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+k,b+k+2)两点且点A在第一象限,是两个函数的一个交点;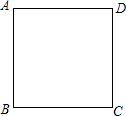 如图,四边形ABCD为正方形.在边AD上取一点E,连接BE,使∠AEB=60°.
如图,四边形ABCD为正方形.在边AD上取一点E,连接BE,使∠AEB=60°. 已知四边形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3,若P为AB边上任意一点,延长PD到E,使DE=2PD,再以PE,PC为边作平行四边形PCQE,则对角线PQ的长的最小值是6.
已知四边形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3,若P为AB边上任意一点,延长PD到E,使DE=2PD,再以PE,PC为边作平行四边形PCQE,则对角线PQ的长的最小值是6.