题目内容
15.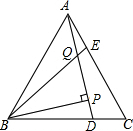 如图,已知在等边△ABC中,D、E是BC,AC上的点,AE=CD,AD与BE相交于Q,BP丄AD,则$\frac{PQ}{BQ}$的值是$\frac{1}{2}$.
如图,已知在等边△ABC中,D、E是BC,AC上的点,AE=CD,AD与BE相交于Q,BP丄AD,则$\frac{PQ}{BQ}$的值是$\frac{1}{2}$.
分析 首先证得△ABE≌△CAD,得∠ABE=∠CAD,又∠BAD+∠CAD=∠BAC=60°,所以∠BQP=∠ABE+∠BAQ=60°,所以,在直角△BPQ中,∠QBP=30°,即可解得.
解答 解:∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠C=60°,
在△ABE和△CAD中,
$\left\{\begin{array}{l}{AB=CA}\\{∠BAE=∠C}\\{AE=CD}\end{array}\right.$,
∴△ABE≌△CAD,
∴∠ABE=∠CAD,
又∵∠BAD+∠CAD=∠BAC=60°,
∴∠BQP=∠ABE+∠BAQ=60°,
又∵BP⊥AD,
∴在直角△BPQ中,∠QBP=30°,
∴BQ=2PQ,
∴$\frac{PQ}{BQ}=\frac{1}{2}$.
故答案为:$\frac{1}{2}$
点评 本题主要考查了等边三角形的性质、三角形外角的性质、含30度直角三角形的性质及全等三角形的判定与性质,考查了学生综合运用知识解答问题的能力.

练习册系列答案
相关题目
 已知,如图,AB∥CD,EF分别交AB、CD于点E、F,EG平分∠AEF,FH平分∠EFD,求证:EG∥FH.
已知,如图,AB∥CD,EF分别交AB、CD于点E、F,EG平分∠AEF,FH平分∠EFD,求证:EG∥FH. 如图,D是△ABC的BC边上的点,BD:DC=2:1,点E是AD的中点,连接BE并延长交AC于点F,求BE:EF的值.
如图,D是△ABC的BC边上的点,BD:DC=2:1,点E是AD的中点,连接BE并延长交AC于点F,求BE:EF的值.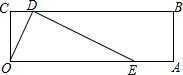 如图,四边形OABC是矩形,OA=3,OC=1,点D是线段BC上的动点(与端点B、C不重合),过点D作直线ED交线段OA于点E,tan∠DEO=$\frac{1}{2}$.若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1,则四边形O1A1B1C1与矩形OABC的重叠部分的面积是$\frac{5}{4}$.
如图,四边形OABC是矩形,OA=3,OC=1,点D是线段BC上的动点(与端点B、C不重合),过点D作直线ED交线段OA于点E,tan∠DEO=$\frac{1}{2}$.若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1,则四边形O1A1B1C1与矩形OABC的重叠部分的面积是$\frac{5}{4}$.
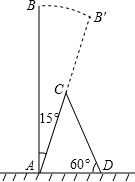 一棵大树树干AB(假定树干AB垂直于地面)被刮倾斜15°后折断在地上,树的项部恰好接触到地面D(如图所示),量得树干的倾斜角为∠BAC=15°,大树被折断部分和地面所成的角∠ADC=60°,AD=3.6米,求这棵大树AB原来的高度是多少米?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4)
一棵大树树干AB(假定树干AB垂直于地面)被刮倾斜15°后折断在地上,树的项部恰好接触到地面D(如图所示),量得树干的倾斜角为∠BAC=15°,大树被折断部分和地面所成的角∠ADC=60°,AD=3.6米,求这棵大树AB原来的高度是多少米?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4) 甲乙两轮船同时从港口A开出,其中甲轮船每小时航行12海里,乙轮船每小时航行16海里,它们离开港口一个半小时后分别位于B,C两处,且相距30海里,如果甲轮船的航行方向为北偏西40°,请你确定乙轮船的航行方向.
甲乙两轮船同时从港口A开出,其中甲轮船每小时航行12海里,乙轮船每小时航行16海里,它们离开港口一个半小时后分别位于B,C两处,且相距30海里,如果甲轮船的航行方向为北偏西40°,请你确定乙轮船的航行方向.