题目内容
20.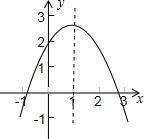 已知二次函数y=ax2+bx+c的图象如图所示,下列说法①a>0;②b2-4ac>0;③4a+2b+c>0;④c<0;⑤b>0.其中正确的有( )
已知二次函数y=ax2+bx+c的图象如图所示,下列说法①a>0;②b2-4ac>0;③4a+2b+c>0;④c<0;⑤b>0.其中正确的有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 采用形数结合的方法解题.根据抛物线的开口方向,对称轴,与x、y轴的交点,x=2的函数值的符号,通过推算进行判断.
解答 解:①∵二次函数y=ax2+bx+c的图象的开口方向是向下,∴a<0;故本选项不正确;
②∵二次函数y=ax2+bx+c的图象与x轴有两个不同的交点,∴△=b2-4ac>0;故本选项正确;
③根据图象知,当x=2时,y>0,即4a+2b+c>0;故本选项正确;
④∵二次函数y=ax2+bx+c的图象与y轴交于正半轴,∴c>0;故本选项不正确;
⑤根据对称轴在y轴的右侧,ab的符号相反,得出b>0,故本选项正确;
综上所述,正确结论共3个;
故选B.
点评 本题考查了二次函数的图象与系数的关系,二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点、抛物线与x轴交点的个数等确定.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
11.有五张形状、大小、质地都相同的卡片,上面分别画有下列图形:①线段,②等边三角形,③平行四边形,④直角三角形,⑤菱形.若将卡片背面朝上并洗匀,则从中任意抽取一张,正面图形既是轴对称图形,又是中心对称图形的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
15.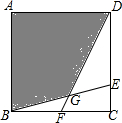 如图,在正方形ABCD中,E在CD边上,F在BC边上,AB=1,DE=2CE,BF=FC,BE与DF交于点G,则图中阴影部分(即四边形ABGD)的面积是( )
如图,在正方形ABCD中,E在CD边上,F在BC边上,AB=1,DE=2CE,BF=FC,BE与DF交于点G,则图中阴影部分(即四边形ABGD)的面积是( )
 如图,在正方形ABCD中,E在CD边上,F在BC边上,AB=1,DE=2CE,BF=FC,BE与DF交于点G,则图中阴影部分(即四边形ABGD)的面积是( )
如图,在正方形ABCD中,E在CD边上,F在BC边上,AB=1,DE=2CE,BF=FC,BE与DF交于点G,则图中阴影部分(即四边形ABGD)的面积是( )| A. | $\frac{9}{14}$ | B. | $\frac{2}{3}$ | C. | $\frac{7}{10}$ | D. | $\frac{3}{4}$ |
9.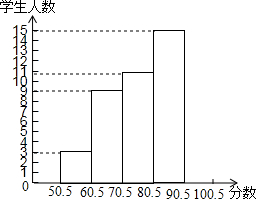 为了了解奥运知识,某中学举行了一次“奥运知识竞赛”,共有900名学生参加了这次竞赛,为了了解本次竞赛情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分),进行统计,请你根据下面尚未完成的统计表和统计图,解答下列问题.
为了了解奥运知识,某中学举行了一次“奥运知识竞赛”,共有900名学生参加了这次竞赛,为了了解本次竞赛情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分),进行统计,请你根据下面尚未完成的统计表和统计图,解答下列问题.
(1)根据以上信息,统计表中A=0.18,B=12,C=0.24;
(2)补全统计图;
(3)在该问题中,个体是每一个学生的竞赛成绩;
(4)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为多少人?
 为了了解奥运知识,某中学举行了一次“奥运知识竞赛”,共有900名学生参加了这次竞赛,为了了解本次竞赛情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分),进行统计,请你根据下面尚未完成的统计表和统计图,解答下列问题.
为了了解奥运知识,某中学举行了一次“奥运知识竞赛”,共有900名学生参加了这次竞赛,为了了解本次竞赛情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分),进行统计,请你根据下面尚未完成的统计表和统计图,解答下列问题.| 分组 | 频数 | 频率 |
| 50.5~60.5 | 3 | 0.06 |
| 60.5~70.5 | 9 | A |
| 70.5~80.5 | 11 | 0.22 |
| 80.5~90.5 | 15 | 0.30 |
| 90.5~100.5 | B | C |
(2)补全统计图;
(3)在该问题中,个体是每一个学生的竞赛成绩;
(4)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为多少人?
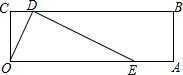 如图,四边形OABC是矩形,OA=3,OC=1,点D是线段BC上的动点(与端点B、C不重合),过点D作直线ED交线段OA于点E,tan∠DEO=$\frac{1}{2}$.若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1,则四边形O1A1B1C1与矩形OABC的重叠部分的面积是$\frac{5}{4}$.
如图,四边形OABC是矩形,OA=3,OC=1,点D是线段BC上的动点(与端点B、C不重合),过点D作直线ED交线段OA于点E,tan∠DEO=$\frac{1}{2}$.若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1,则四边形O1A1B1C1与矩形OABC的重叠部分的面积是$\frac{5}{4}$.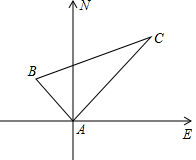 甲乙两轮船同时从港口A开出,其中甲轮船每小时航行12海里,乙轮船每小时航行16海里,它们离开港口一个半小时后分别位于B,C两处,且相距30海里,如果甲轮船的航行方向为北偏西40°,请你确定乙轮船的航行方向.
甲乙两轮船同时从港口A开出,其中甲轮船每小时航行12海里,乙轮船每小时航行16海里,它们离开港口一个半小时后分别位于B,C两处,且相距30海里,如果甲轮船的航行方向为北偏西40°,请你确定乙轮船的航行方向. 矩形ABCD中,E在CD上,将△ADE沿AE折叠,使点D落在边BC上的F处,如果∠EAD=15°,则∠BAF为60°.
矩形ABCD中,E在CD上,将△ADE沿AE折叠,使点D落在边BC上的F处,如果∠EAD=15°,则∠BAF为60°. 如图,在矩形ABCD中,以B为圆心,BC长为半径作弧,交AD于E,连接BE,过C点作CF⊥BE于F.
如图,在矩形ABCD中,以B为圆心,BC长为半径作弧,交AD于E,连接BE,过C点作CF⊥BE于F.