题目内容
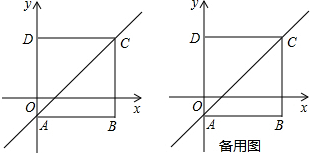
13. 如图,矩形ABCD中,AB=2,BC=3,点P是BC边上任意一点,E,F,R分别是AP,RP,CD的中点,则EF的长为( )
如图,矩形ABCD中,AB=2,BC=3,点P是BC边上任意一点,E,F,R分别是AP,RP,CD的中点,则EF的长为( )| A. | $\frac{\sqrt{13}}{2}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{5}{2}$ |
分析 连接AR,根据勾股定理可求出AR的长,再根据三角形的中位线平行于第三边并且等于第三边的一半可得EF=$\frac{1}{2}$AR,问题得解.
解答 解:连接AR,
∵四边形ABCD是矩形,
∴∠D=90°,AB=DC=2,
∵R是CD的中点,
∴DR=1,
由勾股定理得,AR=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
∵E、F分别是PA、PR的中点,
∴EF是△APR的中位线,
∴EF=$\frac{1}{2}$AR=$\frac{1}{2}$×$\sqrt{10}$=$\frac{\sqrt{10}}{2}$.
故选B.
点评 本题考查了三角形的中位线平行于第三边并且等于第三边的一半,勾股定理,熟记定理是解题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 如图,D是△ABC的BC边上的点,BD:DC=2:1,点E是AD的中点,连接BE并延长交AC于点F,求BE:EF的值.
如图,D是△ABC的BC边上的点,BD:DC=2:1,点E是AD的中点,连接BE并延长交AC于点F,求BE:EF的值.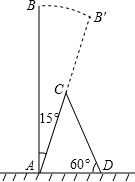 一棵大树树干AB(假定树干AB垂直于地面)被刮倾斜15°后折断在地上,树的项部恰好接触到地面D(如图所示),量得树干的倾斜角为∠BAC=15°,大树被折断部分和地面所成的角∠ADC=60°,AD=3.6米,求这棵大树AB原来的高度是多少米?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4)
一棵大树树干AB(假定树干AB垂直于地面)被刮倾斜15°后折断在地上,树的项部恰好接触到地面D(如图所示),量得树干的倾斜角为∠BAC=15°,大树被折断部分和地面所成的角∠ADC=60°,AD=3.6米,求这棵大树AB原来的高度是多少米?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4)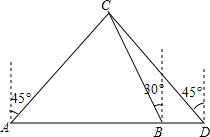 某船向正东航行,在A处望见灯塔C在东北方向,前进到B处望见灯塔C在北偏西30°,又航行了半小时到D处,望见灯塔C恰在西北方向,若船速为每小时20海里.求A、D两点间的距离.(结果不取近似值)
某船向正东航行,在A处望见灯塔C在东北方向,前进到B处望见灯塔C在北偏西30°,又航行了半小时到D处,望见灯塔C恰在西北方向,若船速为每小时20海里.求A、D两点间的距离.(结果不取近似值)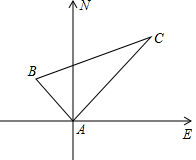 甲乙两轮船同时从港口A开出,其中甲轮船每小时航行12海里,乙轮船每小时航行16海里,它们离开港口一个半小时后分别位于B,C两处,且相距30海里,如果甲轮船的航行方向为北偏西40°,请你确定乙轮船的航行方向.
甲乙两轮船同时从港口A开出,其中甲轮船每小时航行12海里,乙轮船每小时航行16海里,它们离开港口一个半小时后分别位于B,C两处,且相距30海里,如果甲轮船的航行方向为北偏西40°,请你确定乙轮船的航行方向.