题目内容
5．
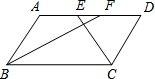如图，在?ABCD中，BF平分∠ABC，交AD于点F，CE平分∠BCD，交AD于点E，AB=6，EF=2，则BC长为（ ）| A． | 8 | B． | 10 | C． | 12 | D． | 14 |
分析 由平行四边形的性质和角平分线得出∠ABF=∠AFB，得出AF=AB=6，同理可证DE=DC=6，再由EF的长，即可求出BC的长．
解答 解：∵四边形ABCD是平行四边形，
∴AD∥BC，DC=AB=6，AD=BC，
∴∠AFB=∠FBC，
∵BF平分∠ABC，
∴∠ABF=∠FBC，
则∠ABF=∠AFB，
∴AF=AB=6，
同理可证：DE=DC=6，
∵EF=AF+DE-AD=2，
即6+6-AD=2，
解得：AD=10；
故选：B．
点评 本题主要考查了平行四边形的性质、等腰三角形的判定；熟练掌握平行四边形的性质，证出AF=AB是解决问题的关键．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
15．如图是某地2月18日到23日PM2.5浓度和空气质量指数AQI的统计图（当AQI不大于100时称空气质量为“优良”），由图可得下列说法：①18日的PM2.5浓度最低；②这六天中PM2.5浓度的中位数是112?g/cm2；③这六天中有4天空气质量为“优良”；④空气质量指数AQI与PM2.5浓度有关，其中正确的说法是（ ）
| A． | ①②③ | B． | ①②④ | C． | ①③④ | D． | ②③④ |
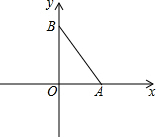如图，在平面直角坐标系中，A、B两点分别在x轴、y轴上，OA=3，OB=4，连接AB．点P在平面内，若以点P、A、B为顶点的三角形与△AOB全等（点P与点O不重合），则点P的坐标为（3，4）或（$\frac{96}{25}$，$\frac{72}{25}$）或（-$\frac{21}{25}$，$\frac{28}{25}$）．
17．等腰三角形有一个角是90°，则另两个角分别是（ ）
| A． | 30°，60° | B． | 45°，45° | C． | 45°，90° | D． | 20°，70° |
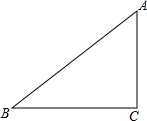如图，在△ABC中，∠ACB=90°，AB=5，BC=4，将△ABC绕点C顺时针旋转90°，若点A，B的对应点分别是点D，E，画出旋转后的三角形，并求点A与点D之间的距离．（不要求尺规作图）