题目内容
16.【发现】如图1∠ACB=∠ADB=90°,那么点D在经过A,B,C三点的圆上(如图1①)
【思考】
如图1②,如果∠ACB=∠ADB=a(a≠90°)(点C,D在AB的同侧),那么点D还在经过A,B,C三点的圆上吗?图中卡通人证明了D不在⊙O外,请你画图证明点D也不在⊙O内.
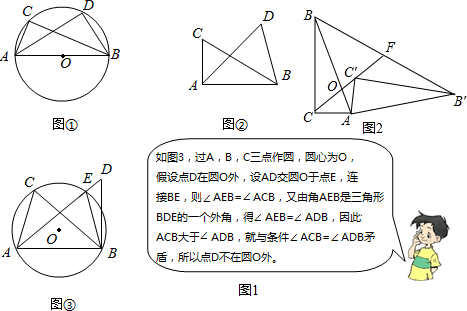
【应用】:利用【发现】和【思考】中的结论解决以下问题:
如图2,在Rt△ACB中,∠ACB=90°,CA=6,$cos∠CAB=\frac{1}{3}$,若将△ACB绕点A顺时针旋转得Rt△AC′B′,旋转角为α(0°≤α≤180°)连结CC′交BB′于点F,交AB边于点O.
(1)请证明:∠BFO=∠CAO.
(2)若CA=CO=6,求则OF的长.
(3)在运动过程中,请证明F永远是BB′的中点,并直接写出点F的运动路线长.
分析 【思考】假设点D在⊙O内,利用圆周角定理及三角形外角的性质,可证得与条件相矛盾的结论,从而证得点D不在⊙O内;
【应用】:(1)过C作CD⊥AB于点D,BH⊥CF于H,由已知条件得到AD=DO,解直角三角形得到AD=$\frac{1}{3}$AC=2,得到BO=AB-AO=18-4=14,
根据旋转的性质得到AC=AC′,AB=AB′,∠CAC′=∠BAB′,推出A,F,B,C四点共圆,于是得到结论;(2)由等腰三角形的性质得到∠COA=∠CAO,根据三角形的内角和得到∠BOF=∠BFO,根据等腰三角形的性质得到BF=BO=14,于是得到结论;
(3)连接AF,根据圆周角定理得到∠ABC=∠AFC根据等腰三角形的性质得到F永远是BB′的中点;根据圆周角定理得到在运动过程中,点F的运动路线是以AB为直径的半圆,即可得到结论.
解答 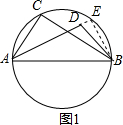 解:【思考】如图1,假设点D在⊙O内,延长AD交⊙O于点E,连接BE,则∠AEB=∠ACB,
解:【思考】如图1,假设点D在⊙O内,延长AD交⊙O于点E,连接BE,则∠AEB=∠ACB,
∵∠ADB是△BDE的外角,
∴∠ADB>∠AEB,
∴∠ADB>∠ACB,
因此,∠ADB>∠ACB这与条件∠ACB=∠ADB矛盾,
∴点D也不在⊙O内,
∴点D即不在⊙O内,也不在⊙O外,点D在⊙O上;
【应用】:(1)如图2,过C作CD⊥AB于点D,BH⊥CF于H,
∵CA=CO,
∴AD=DO,
在Rt△ACB中,cos∠CAB=$\frac{1}{3}$=$\frac{AC}{AB}$=$\frac{6}{AB}$,
∴AB=3AC=18,
在Rt△ADC中:cos∠CAB=$\frac{1}{3}$=$\frac{AD}{AC}$,
∴AD=$\frac{1}{3}$AC=2,
∴AO=2AD=4,
∴BO=AB-AO=18-4=14,
∵△AC′B′是由△ACB旋转得到,
∴AC=AC′,AB=AB′,∠CAC′=∠BAB′,
∵∠ACC′=$\frac{1}{2}$(180°-∠CAC′),∠ABB′=$\frac{1}{2}$(180°-∠BAB′),
∴∠ABB′=∠ACC′,
∴A,F,B,C四点共圆,
∴∠BFO=∠CAO;
(2)∵CA=CO,
∴∠COA=∠CAO,
又∵∠COA=∠BOF(对顶角相等),
∴∠BOF=∠BFO,
∴BF=BO=14,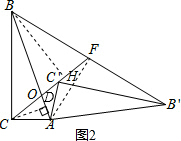
∵$cos∠CAB=\frac{1}{3}$,
∴HF=$\frac{7\sqrt{10}}{5}$,
∴OF=2HF=$\frac{14\sqrt{10}}{5}$;
(3)如图2,连接AF,
∵A,F,B,C四点共圆,
∴∠ABC=∠AFC,
∵∠ABC+∠CAB=90°,
∴∠BFO+∠AFC=90°,
∴AF⊥BB′,
∵AB=AB′,
∴BF=B′F;
∴F永远是BB′的中点;
∵∠AFB=90°,
∴在运动过程中,点F的运动路线是以AB为直径的半圆,
∵CA=6,$cos∠CAB=\frac{1}{3}$,
∴AB=18,
∴点F的运动路线长=$\frac{1}{2}$×18π=9π.
点评 本题综合考查了圆周角定理、反证法、三角形外角的性质、三角形的内角和定理,点和圆的位置关系、切线的判定、矩形的判定和性质以及解直角三角形等知识,熟练掌握性质定理是解题的关键.

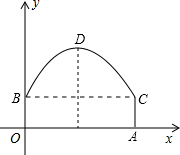 如图,东湖隧道的截面由抛物线和长方形构成,长方形的长OA为12m,宽OB为4m,隧道顶端D到路面的距离为10m,建立如图所示的直角坐标系
如图,东湖隧道的截面由抛物线和长方形构成,长方形的长OA为12m,宽OB为4m,隧道顶端D到路面的距离为10m,建立如图所示的直角坐标系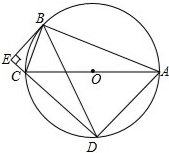 如图,⊙O是△ABC的外接圆,∠ABC=90°,BE⊥CE,BE是⊙O的切线交DC的延长线于点E.
如图,⊙O是△ABC的外接圆,∠ABC=90°,BE⊥CE,BE是⊙O的切线交DC的延长线于点E.

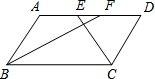 如图,在?ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为( )
如图,在?ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为( )