题目内容
13．若反比例函数的图象过点（3，-2），则其函数表达式为y=-$\frac{6}{x}$．分析 设反比例函数解析式为y=$\frac{k}{x}$（k为常数，且k≠0），由点的坐标利用反比例函数图象上点的坐标特征求出k值，由此即可得出结论．
解答 解：设反比例函数解析式为y=$\frac{k}{x}$（k为常数，且k≠0），
∵该函数图象过点（3，-2），
∴k=3×（-2）=-6．
∴该反比例函数解析式为y=-$\frac{6}{x}$．
故答案为：y=-$\frac{6}{x}$．
点评 本题考查了反比例函数图象上点的坐标特征，解题的关键是求出反比例函数系数k．本题属于基础题，难度不大，解决该题型题目时，根据点的坐标利用反比例函数图象上点的坐标特征求出系数k是关键．
练习册系列答案
相关题目
3．计算正确的是（ ）
| A． | $\root{3}{1}=±1$ | B． | $\sqrt{{{（{-3}）}^2}}=3$ | C． | $-\sqrt{0.81}=0.9$ | D． | $\sqrt{9}=±3$ |
如图，正方形ABCD的边长为2，点E，F分别在边AD，CD上，若∠EBF=45°，则△EDF的周长等于4．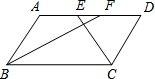
如图，在?ABCD中，BF平分∠ABC，交AD于点F，CE平分∠BCD，交AD于点E，AB=6，EF=2，则BC长为（ ）