题目内容
15．如图是某地2月18日到23日PM2.5浓度和空气质量指数AQI的统计图（当AQI不大于100时称空气质量为“优良”），由图可得下列说法：①18日的PM2.5浓度最低；②这六天中PM2.5浓度的中位数是112?g/cm2；③这六天中有4天空气质量为“优良”；④空气质量指数AQI与PM2.5浓度有关，其中正确的说法是（ ）
| A． | ①②③ | B． | ①②④ | C． | ①③④ | D． | ②③④ |
分析 利用折线统计图1可判断18日对应的PM2.5浓度的值最小，则可①进行判断；利用折线统计图1得到6个PM2.5浓度值，然后根据中位数的定义计算出这组数据的中位数，则可对②进行判断；利用折线统计图2找出AQI不大于100的数据可对③进行判断；结合两个折线统计图，比较每天的PM2.5浓度和空气质量指数AQI可对④进行判断．
解答 解：18日的PM2.5浓度最低，为25，所以①正确；
这六天中PM2.5浓度的值为25，66，67，92，144，158，它的中位数是$\frac{1}{2}$（67+92）=79.5，所以②错误；
这六天中，18日、19日、20日、23日的空气质量为“优良”，所以③正确；
空气质量指数AQI与PM2.5浓度有关，PM2.5浓度越大，空气质量指数AQI越大，所以④正确．
故选C．
点评 本题考查了折线统计图：折线图是用一个单位表示一定的数量，根据数量的多少描出各点，然后把各点用线段依次连接起来．以折线的上升或下降来表示统计数量增减变化．折线图不但可以表示出数量的多少，而且能够清楚地表示出数量的增减变化情况．
练习册系列答案
相关题目
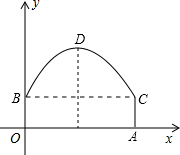如图，东湖隧道的截面由抛物线和长方形构成，长方形的长OA为12m，宽OB为4m，隧道顶端D到路面的距离为10m，建立如图所示的直角坐标系
3．计算正确的是（ ）
| A． | $\root{3}{1}=±1$ | B． | $\sqrt{{{（{-3}）}^2}}=3$ | C． | $-\sqrt{0.81}=0.9$ | D． | $\sqrt{9}=±3$ |
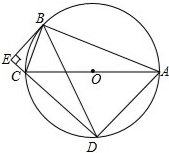如图，⊙O是△ABC的外接圆，∠ABC=90°，BE⊥CE，BE是⊙O的切线交DC的延长线于点E．
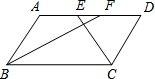如图，在?ABCD中，BF平分∠ABC，交AD于点F，CE平分∠BCD，交AD于点E，AB=6，EF=2，则BC长为（ ）