题目内容
14.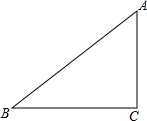 如图,在△ABC中,∠ACB=90°,AB=5,BC=4,将△ABC绕点C顺时针旋转90°,若点A,B的对应点分别是点D,E,画出旋转后的三角形,并求点A与点D之间的距离.(不要求尺规作图)
如图,在△ABC中,∠ACB=90°,AB=5,BC=4,将△ABC绕点C顺时针旋转90°,若点A,B的对应点分别是点D,E,画出旋转后的三角形,并求点A与点D之间的距离.(不要求尺规作图)
分析 首先根据题意画出旋转后的三角形,易得△ACD是等腰直角三角形,然后由勾股定理求得AC的长.
解答  解:如图,∵在△ABC中,∠ACB=90°,AB=5,BC=4,
解:如图,∵在△ABC中,∠ACB=90°,AB=5,BC=4,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=3,
∵将△ABC绕点C顺时针旋转90°,点A,B的对应点分别是点D,E,
∴AC=CD=3,∠ACD=90°,
∴AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=3$\sqrt{2}$.
点评 此题考查了旋转的性质以及勾股定理.注意掌握旋转前后图形的对应关系是解此题的关键.

练习册系列答案
相关题目
9.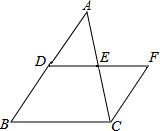 如图,DE是△ABC的中位线,过点C作CF∥BD交DE的延长线于点F,则下列结论正确的是( )
如图,DE是△ABC的中位线,过点C作CF∥BD交DE的延长线于点F,则下列结论正确的是( )
 如图,DE是△ABC的中位线,过点C作CF∥BD交DE的延长线于点F,则下列结论正确的是( )
如图,DE是△ABC的中位线,过点C作CF∥BD交DE的延长线于点F,则下列结论正确的是( )| A. | EF=CF | B. | EF=DE | C. | CF<BD | D. | EF>DE |

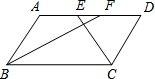 如图,在?ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为( )
如图,在?ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为( )