题目内容
2.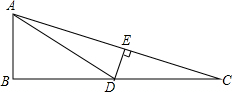 如图,△ABC中,DE垂直平分AC,与AC交于E,与BC交于D,∠C=15°,∠BAD=60°.若CD=1,求AB的长度.
如图,△ABC中,DE垂直平分AC,与AC交于E,与BC交于D,∠C=15°,∠BAD=60°.若CD=1,求AB的长度.
分析 根据线段垂直平分线的性质得到DA=DC=1,根据三角形的外角的性质得到∠ADB=30°,根据直角三角形的性质得到答案.
解答 解:∵DE垂直平分AC,
∴DA=DC=1,
∴∠DAC=∠C=15°,
∴∠ADB=30°,又∠BAD=60°,
∴∠B=90°,又∠ADB=30°,
∴AB=$\frac{1}{2}$AD=$\frac{1}{2}$.
点评 本题考查的是线段垂直平分线的性质和直角三角形的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
相关题目
12.等边三角形ABC的两条角平分线BD和CE相交所夹锐角的度数为( )
| A. | 75° | B. | 60° | C. | 45° | D. | 30° |
10.如果a,b互为相反数,那么(5a2-10a)-5(a2+2b-3)的值为( )
| A. | -10 | B. | 5 | C. | 15 | D. | -15 |
 △ABC中,∠ABC=120°,以AC为边向形外作等边三角形ACD,求证:BD=AB+BC.
△ABC中,∠ABC=120°,以AC为边向形外作等边三角形ACD,求证:BD=AB+BC.