题目内容
16.将下列分式约分(1)$\frac{{10{a^3}bc}}{{-5{a^2}{b^3}{c^2}}}$;
(2)$\frac{-2a(a+b)}{3b(a+b)}$;
(3)$\frac{{{{(a-x)}^2}}}{{{{(x-a)}^3}}}$;
(4)$\frac{{{x^2}-25}}{{{x^2}-10x+25}}$.
分析 (1)根据分式的基本性质,分子分母同时除以
(2)约去分母、分子中的公因式(a+b)即可;
(3)先把分子中的(a-x)2转变成(x-a)2,再分子、分母约分即可;
(4)根据平方差公式进行因式分解,再约分即可.
解答 解:(1)$\frac{{10{a^3}bc}}{{-5{a^2}{b^3}{c^2}}}$=-$\frac{2a}{{b}^{2}c}$;
(2)$\frac{-2a(a+b)}{3b(a+b)}$=-$\frac{2a}{3b}$;
(3)$\frac{{{{(a-x)}^2}}}{{{{(x-a)}^3}}}$=$\frac{(x-a)^{2}}{(x-a)^{3}}$=$\frac{1}{x-a}$;
(4)$\frac{{{x^2}-25}}{{{x^2}-10x+25}}$=$\frac{(x+5)(x-5)}{(x-5)^{2}}$=$\frac{x+5}{x-5}$.
点评 此题考查了约分,用到的知识点是因式分解、分式的基本性质,在约分时要注意符号的变化.

练习册系列答案
相关题目
11.下列命题中,正确的是( )
| A. | 两条对角线互相平分的四边形是平行四边形 | |
| B. | 两条对角线互相垂直的四边形是菱形 | |
| C. | 两条对角线互相垂直且相等的四边形是正方形 | |
| D. | 两条对角线相等的四边形是矩形 |
5.已知OA⊥OC,∠AOB:∠AOC=2:3,则∠BOC的度数为( )
| A. | 30 | B. | 150 | C. | 30或150 | D. | 以上都不对 |
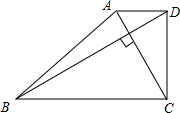 如图,在四边形ABCD中,AD∥BC,AC⊥BD.
如图,在四边形ABCD中,AD∥BC,AC⊥BD.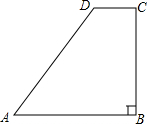 如图,在直角梯形ABCD中,∠DCB=90°,AB∥CD,AB=25,BC=24.将该梯形沿过B点的直线折叠,使A点恰好与D点重合,BE为折痕.
如图,在直角梯形ABCD中,∠DCB=90°,AB∥CD,AB=25,BC=24.将该梯形沿过B点的直线折叠,使A点恰好与D点重合,BE为折痕.