题目内容
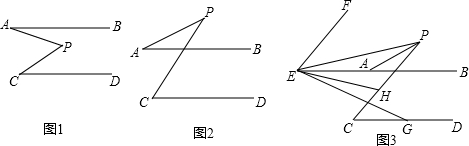
 一架云梯长25米,如图所示,斜靠在一面墙上,这时梯子的顶端距地面24米.
一架云梯长25米,如图所示,斜靠在一面墙上,这时梯子的顶端距地面24米.(1)求这个梯子的底部离墙的垂直距离有多远?
(2)如果梯子的顶端下滑4米,那么梯子的底部在水平方向也滑动了4米吗?为什么?
(3)当梯子的顶端下滑的距离与梯子的底部水平滑动的距离相等时,这时梯子的顶端距地面有多高?
考点:勾股定理的应用
专题:
分析:(1)利用勾股定理计算出BO的长即可;
(2)首先计算出DO的长,然后再利用DO-BO即可;
(3)设梯子的顶端下滑的距离与梯子的底部水平滑动的距离为x米,根据题意勾股定理可得:(24-x)2+(7+x)2=252,解出x的值,可得答案.
(2)首先计算出DO的长,然后再利用DO-BO即可;
(3)设梯子的顶端下滑的距离与梯子的底部水平滑动的距离为x米,根据题意勾股定理可得:(24-x)2+(7+x)2=252,解出x的值,可得答案.
解答:解:(1)由题意得:AO=24米,AB=25米,
BO=
=7(米),
答:这个梯子的底部离墙的垂直距离有7米;
(2)∵梯子的顶端下滑4米,
∴CO=20米,
∴DO=
=15(米),
∴DB=15-7=8(米),
∴梯子的底部在水平方向也滑动了8米;
(3)设梯子的顶端下滑的距离与梯子的底部水平滑动的距离为x米,
由题意得:(24-x)2+(7+x)2=252,
解得:x1=17,x2=0(不合题意舍去),
24-17=7(米),
答:梯子的顶端距地面有7米.
BO=
| 252-242 |
答:这个梯子的底部离墙的垂直距离有7米;
(2)∵梯子的顶端下滑4米,
∴CO=20米,
∴DO=
| 252-202 |
∴DB=15-7=8(米),
∴梯子的底部在水平方向也滑动了8米;
(3)设梯子的顶端下滑的距离与梯子的底部水平滑动的距离为x米,
由题意得:(24-x)2+(7+x)2=252,
解得:x1=17,x2=0(不合题意舍去),
24-17=7(米),
答:梯子的顶端距地面有7米.
点评:此题主要考查了勾股定理的应用,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
相关题目
下列方程组不是三元一次方程组的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
在△ABC中,∠C=90°,BC=2,
=
,则边AC的长是( )
| BC |
| AB |
| 2 |
| 3 |
A、
| ||
| B、3 | ||
C、
| ||
D、
|
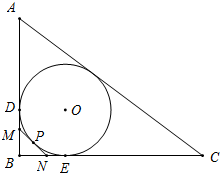 如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若AB=5cm,AC=13cm,则Rt△MBN的周长为
如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若AB=5cm,AC=13cm,则Rt△MBN的周长为