题目内容
14.正方形ABCD,45°的三角板BEF顶点放在B旋转,两边分别交AD、DC于P、Q.(1)判断PQ,AP,CQ关系,并证明;
(2)判断∠CQB和∠BQP大小关系,并证明.
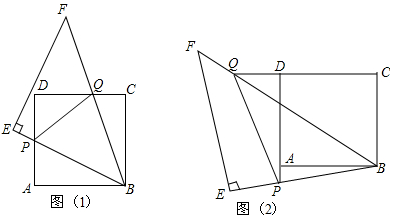
分析 (1)延长PA到H,使AH=CQ,连结PQ,先利用“SAS”可判断△ABH≌△CBQ,则BH=BQ,∠HBA=∠QBC,由于∠PBQ=45°,∠ABH+∠ABP=45°,得到∠HBP=∠PBQ,然后再根据“SAS”证明△PBH≌△PBQ,则PH=PQ,即HA+PA=PQ,所以PQ=CQ+AP;
(2)在DN上截取DH=BM,与(1)同理先证明△BCH≌△BAP,得到BH=BP,∠CBH=∠ABP,再利用“SAS”证明∴△PBQ≌△HBQ,得到∠CQB=∠BQP.
解答  (1)解:PQ=CQ+AP;
(1)解:PQ=CQ+AP;
理由:延长PA到H,使AH=CQ,连结PQ,如图1,
∵四边形ABCD为正方形,
∴∠C=∠BAD=90°,BC=AB,
在△ABH和△CBQ中,
$\left\{\begin{array}{l}{AB=BC}\\{∠BAH=∠BCQ}\\{AH=CQ}\end{array}\right.$,
∴△ABH≌△CBQ(SAS),
∴BH=BQ,∠HBA=∠QBC,
∵∠PBQ=45°,
∴∠QBC+∠ABP=45°,
∴∠ABH+∠ABP=45°,
∴∠HBP=∠PBQ,
在△PBH和△PBQ中,
$\left\{\begin{array}{l}{BH=BQ}\\{∠HBP=∠QBP}\\{PB=PB}\end{array}\right.$,
∴△PBH≌△PBQ(SAS),
∴PH=PQ,即HA+PA=PQ,
∴PQ=CQ+AP;
(2)解:∠CQB=∠BQP.理由如下:
在DC上截取CH=AP,如图(2),
与(1)一样可证明△BCH≌△BAP,
∴BH=BP,∠CBH=∠ABP,
∵∠PBQ=45°,
∴∠PBA+∠ABQ=45°,
∴∠HBC+∠ABQ=45°,
∴∠HBQ=45°,
∴∠PBQ=∠HBQ,
在△PBQ和△HBQ中,
$\left\{\begin{array}{l}{PB=HB}\\{∠PBQ=∠HBQ}\\{BQ=BQ}\end{array}\right.$,
∴△PBQ≌△HBQ(SAS),
∴∠CQB=∠BQP.
点评 本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.也考查了等腰三角形的性质.也考查了正方形的性质.
