题目内容
3.甲、乙两个同学分别解一道一元二次方程x2+bx+c=0,甲因把一次项系数看错了,而解得方程两根为-3和5,乙把常数项看错了,解得两根为2和2,则原方程是x2-4x-15=0.分析 根据根与系数的方程,由甲把一次项系数看错可得到常数项c,由乙把常数项看错可得到一次项系数b,于是可确定原一元二次方程.
解答 解:∵甲因把一次项系数看错了,而解得方程两根为-3和5,
∴-3×5=c,即c=-15,
∵乙把常数项看错了,解得两根为2和2,
∴2+2=-b,即b=-4,
∴原方程为x2-4x-15=0.
故答案为x2-4x-15=0.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
11.某商店举办有奖储蓄活动,购货满100元者发兑奖券一张,在10000张奖券中,设特等奖1个,一等奖10个,二等奖100个.若某人购物满100元,那么他中一等奖的概率是( )
| A. | $\frac{1}{100}$ | B. | $\frac{1}{1000}$ | C. | $\frac{1}{10000}$ | D. | $\frac{111}{10000}$ |
18.式子$\frac{2x+1}{\sqrt{x-1}}$有意义的x的取值范围是( )
| A. | x<1 | B. | x≠1 | C. | x≥1 | D. | x>1 |
15.如图,小明的父母出去散步,从家走了20分钟到一个离家900米的报亭,母亲随即按原速度返回家,父亲在报亭看了10分钟报纸后,用15分钟返回家,则分别表示父亲、母亲离家距离与时间之间关系的是( )
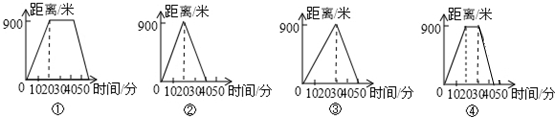

| A. | ①③ | B. | ①② | C. | ④② | D. | ④③ |
12.$\sqrt{(-5)^{2}}$化简后的结果是( )
| A. | $\sqrt{5}$ | B. | 5 | C. | ±$\sqrt{5}$ | D. | -5 |
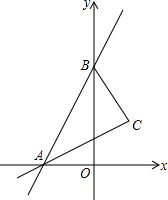 如图,直线y=7x+7交x轴于点A,交y轴于点B.
如图,直线y=7x+7交x轴于点A,交y轴于点B.