题目内容
4.已知x1,x2是方程x2+6x-2=0的两个根,则$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{x}_{1}}{{x}_{2}}$=-20.分析 先根据根与系数的关系得到x1+x2=-6,x1x2=-2,再把原式通分后利用完全平方公式变形得到$\frac{({x}_{1}+{x}_{2})^{2}-2{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}}$,然后利用整体代入的方法计算.
解答 解:根据题意得x1+x2=-6,x1x2=-2,
所以原式=$\frac{{{x}_{1}}^{2}+{{x}_{2}}^{2}}{{x}_{1}{x}_{2}}$=$\frac{({x}_{1}+{x}_{2})^{2}-2{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{(-6)^{2}-2×(-2)}{-2}$=-20.
故答案为-20.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
相关题目
15.如图,小明的父母出去散步,从家走了20分钟到一个离家900米的报亭,母亲随即按原速度返回家,父亲在报亭看了10分钟报纸后,用15分钟返回家,则分别表示父亲、母亲离家距离与时间之间关系的是( )
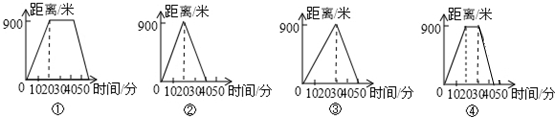

| A. | ①③ | B. | ①② | C. | ④② | D. | ④③ |
12.$\sqrt{(-5)^{2}}$化简后的结果是( )
| A. | $\sqrt{5}$ | B. | 5 | C. | ±$\sqrt{5}$ | D. | -5 |
19.某市2013年投入教育经费2亿元,为了发展教育事业,该市每年教育经费的年增长率均为x,从2013年到2015年共投入教育经费9.5亿元,则下列方程正确的是( )
| A. | 2x2=9.5 | B. | 2(1+x)=9.5 | ||
| C. | 2(1+x)2=9.5 | D. | 2+2(1+x)+2(1+x)2=9.5 |
9.计算:(6a3b4)÷(3a2b)=( )
| A. | 2 | B. | 2ab3 | C. | 3ab3 | D. | 2a5b5 |