题目内容
2.解方程:(1)(40-2x)(26-x)=144×6;
(2)(x-120)[120-(x-120)]=3200;
(3)x2+(x+2)2=3(x-2)2-25;
(4)200(1+x%)×150(1-$\frac{10}{9}$x%)=20000.
分析 (1)先把方程整理成x2-46x+88=0,再根据因式分解的步骤进行因式分解,即可求出x的值.
(2)先设x-120=y,则原方程可化得y2-120y+3200=0,求得y的值,代入求出x的值即可.
(3)先把方程整理成x2-16x-17=0,再根据因式分解的步骤进行因式分解,即可求出x的值.
(4)先设x%=y,则原方程可化得10y2+y-3=0,求得y的值,代入求出x的值即可.
解答 解:(1)(40-2x)(26-x)=144×6;
整理得:x2-46x+88=0,
∴(x-44)(x-2)=0,
∴x1=44,x2=2.
(2)(x-120)[120-(x-120)]=3200;
设x-120=y,则原方程可化得y2-120y+3200=0,
解这个方程得y1=40,y2=80.
当y=40时,x-120=40,∴x1=160,
当y=80时,x-120=80,∴x2=200
∴原方程的解是x1=160,x2=200.
(3)x2+(x+2)2=3(x-2)2-25;
整理得:x2-16x-17=0,
∴(x-17)(x+1)=0,
∴x1=17,x2=-1.
(4)200(1+x%)×150(1-$\frac{10}{9}$x%)=20000.
设x%=y,则原方程可化得10y2+y-3=0,
解这个方程得y1=$\frac{1}{2}$,y2=-$\frac{3}{5}$.
当y=$\frac{1}{2}$时,x%=$\frac{1}{2}$,∴x1=50,
当y=-$\frac{3}{5}$时,x%=-$\frac{3}{5}$,∴x2=-60,
∴原方程的解是x1=50,x2=-60.
点评 本题考查了利用因式分解法把一元二次方程转化为两个一元一次方程求解的能力.要熟练掌握因式分解的方法和换元法是解题的关键.

| A. | $\frac{1}{100}$ | B. | $\frac{1}{1000}$ | C. | $\frac{1}{10000}$ | D. | $\frac{111}{10000}$ |
| A. | $\sqrt{5}$ | B. | 5 | C. | ±$\sqrt{5}$ | D. | -5 |
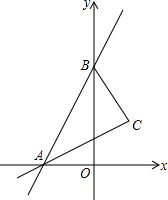 如图,直线y=7x+7交x轴于点A,交y轴于点B.
如图,直线y=7x+7交x轴于点A,交y轴于点B.