题目内容
9.(1)先化简,再求值:x(x+4)+(x-2)2,其中x=$\sqrt{2}$;(2)解方程:$\frac{x}{x-2}$-$\frac{1}{{x}^{2}-4}$=1.
分析 (1)先化简多项式,再代入求值即可解答;
(2)按照解分式方程的步骤,即可解答.
解答 解:(1)x(x+4)+(x-2)2,
=x2+4x+x2-4x+4
=2x2+4,
当x=$\sqrt{2}$时,
原式=$2×(\sqrt{2})^{2}$+4
=4+4
=8.
(2)在方程两边同乘x2-4得:x(x+2)-1=x2-4
解得:x=-$\frac{3}{2}$,
当x=-$\frac{3}{2}$时,x2-4≠0,
故分式方程的解为:x=-$\frac{3}{2}$.
点评 本题考查了解分式方程,解决本题的关键是熟记解分式方程的步骤.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.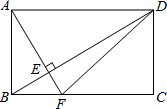 如图,在矩形ABCD中,AF⊥BD于E,AF交BC于点F,连接DF,则图中面积相等但不全等的三角形共有( )
如图,在矩形ABCD中,AF⊥BD于E,AF交BC于点F,连接DF,则图中面积相等但不全等的三角形共有( )
 如图,在矩形ABCD中,AF⊥BD于E,AF交BC于点F,连接DF,则图中面积相等但不全等的三角形共有( )
如图,在矩形ABCD中,AF⊥BD于E,AF交BC于点F,连接DF,则图中面积相等但不全等的三角形共有( )| A. | 2对 | B. | 3对 | C. | 4对 | D. | 5对 |
14. 一个简单空间几何体的三视图如图所示,则这个几何体是( )
一个简单空间几何体的三视图如图所示,则这个几何体是( )
 一个简单空间几何体的三视图如图所示,则这个几何体是( )
一个简单空间几何体的三视图如图所示,则这个几何体是( )| A. | 三棱锥 | B. | 四棱锥 | C. | 三棱柱 | D. | 四棱柱 |
 如图,Rt△ABC的直角边BC在x轴上,斜边AC上的中线BD交y轴于点E,双曲线的y=$\frac{k}{x}$(k>0)图象经过点A,若△BEC的面积为4,则k=8.
如图,Rt△ABC的直角边BC在x轴上,斜边AC上的中线BD交y轴于点E,双曲线的y=$\frac{k}{x}$(k>0)图象经过点A,若△BEC的面积为4,则k=8.
 二次函数y=ax2+bx+c的图象如图所示,判断a,b,c,2a+b,a+b+c,a-b+c的符号.
二次函数y=ax2+bx+c的图象如图所示,判断a,b,c,2a+b,a+b+c,a-b+c的符号.