题目内容
19. 二次函数y=ax2+bx+c的图象如图所示,判断a,b,c,2a+b,a+b+c,a-b+c的符号.
二次函数y=ax2+bx+c的图象如图所示,判断a,b,c,2a+b,a+b+c,a-b+c的符号.
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而得出结论.
解答 解:图象开口向上,与y轴交于负半轴,对称轴在y轴右侧,能得到:a>0,c<0,-$\frac{b}{2a}$>0,b<0;
∵0<-$\frac{b}{2a}$<1,a>0,
∴-b<2a,
∴2a+b>0;
根据图示知,当x=1时,y<0,当x=-1时,y>0,
∴a+b+c<0,a-b+c>0.
点评 主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换.

练习册系列答案
相关题目
7.下列图形中,不是中心对称图形的是( )
| A. | 等边三角形 | B. | 平行四边形 | C. | 菱形 | D. | 矩形 |
11.若x1,x2是x2-x-3=0的两个实数根,则-x1-x2=( )
| A. | ±1 | B. | -3 | C. | -1 | D. | 3 |
8.某瓷砖厂设计了几种瓷砖方案.如图所示,其中是轴对称图形的个数是( )


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
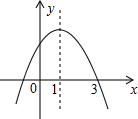 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现有下列结论: