题目内容
1. 如图,Rt△ABC的直角边BC在x轴上,斜边AC上的中线BD交y轴于点E,双曲线的y=$\frac{k}{x}$(k>0)图象经过点A,若△BEC的面积为4,则k=8.
如图,Rt△ABC的直角边BC在x轴上,斜边AC上的中线BD交y轴于点E,双曲线的y=$\frac{k}{x}$(k>0)图象经过点A,若△BEC的面积为4,则k=8.
分析 由BD为Rt△ABC斜边AC上的中线,可得出BD=CD=AD,进而得出∠DCB=∠DBC,再由EO⊥BC得出∠BOE=CBA,从而得出△BOE∽△CBA,由相似三角形的性质可得出$\frac{OE}{BA}=\frac{OB}{BC}$,再结合△BEC的面积为4以及反比例函数系数k的几何意义即可得出结论.
解答 解:∵BD为Rt△ABC斜边AC上的中线,
∴BD=CD=AD,
∴∠DCB=∠DBC,
又∵EO⊥BC,
∴∠BOE=CBA=90°,
∴△BOE∽△CBA,
∴$\frac{OE}{BA}=\frac{OB}{BC}$,
即BC•OE=OB•BA.
又∵S△BCE=$\frac{1}{2}$BC•OE=4,
∴OB•BA=|k|=8,
∴k=±8,
∵k>0,
∴k=8.
故答案为8.
点评 本题考查了反比例函数系数k的几何意义、相似三角形的判定及性质,解题的关键是找出$\frac{OE}{BA}=\frac{OB}{BC}$.本题属于基础题,难度不大,解决该题型题目时,根据相似三角形的性质找出各边的比例关系,再结合三角形的面积公式以及反比例函数系数k的几何意义得出结论.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
6.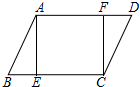 在?ABCD中,AB=5,BC=7,E,F分别为边BC,AD上的点,若四边形AECF为正方形,则AE的长为( )
在?ABCD中,AB=5,BC=7,E,F分别为边BC,AD上的点,若四边形AECF为正方形,则AE的长为( )
 在?ABCD中,AB=5,BC=7,E,F分别为边BC,AD上的点,若四边形AECF为正方形,则AE的长为( )
在?ABCD中,AB=5,BC=7,E,F分别为边BC,AD上的点,若四边形AECF为正方形,则AE的长为( )| A. | 5 | B. | 4或5 | C. | 3或4 | D. | 5或7 |
13.一元二次方程x2-4x+2=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
11.若x1,x2是x2-x-3=0的两个实数根,则-x1-x2=( )
| A. | ±1 | B. | -3 | C. | -1 | D. | 3 |
 四边形ABCD的对角线AC、BD相交于点O,AD∥BC,AC=BD.试添加一个条件AB∥CD(答案不唯一),使四边形ABCD为矩形.
四边形ABCD的对角线AC、BD相交于点O,AD∥BC,AC=BD.试添加一个条件AB∥CD(答案不唯一),使四边形ABCD为矩形.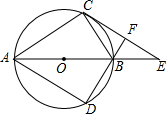 如图,四边形ACBD是⊙O的内接四边形,AB为直径,过C作⊙O的切线交AB的延长于E,DB⊥CE,垂足为F.
如图,四边形ACBD是⊙O的内接四边形,AB为直径,过C作⊙O的切线交AB的延长于E,DB⊥CE,垂足为F.