题目内容
1. 如图,小明的爸爸在鱼池边开了一块四边形土地种了一些蔬菜,爸爸让小明计算一下土地的面积,以便计算一下产量.小明找了一卷米尺,测得AB=4米,BC=3米,CD=13米,DA=12米,又已知∠B=90°.你能够计算这块地的面积吗?
如图,小明的爸爸在鱼池边开了一块四边形土地种了一些蔬菜,爸爸让小明计算一下土地的面积,以便计算一下产量.小明找了一卷米尺,测得AB=4米,BC=3米,CD=13米,DA=12米,又已知∠B=90°.你能够计算这块地的面积吗?
分析 先把解四边形的问题转化成解三角形的问题,再用勾股定理求出AC的长,进而得出四边形面积.
解答 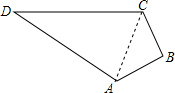 解:连结AC.
解:连结AC.
在Rt△ABC中,
∵AC2=AB2+BC2,AB=4,BC=3,
∴AC=$\sqrt{{4^2}+{3^2}}=5$,
∵AC2=25,AD2=144,DC2=169,
∴25+144=169,
∴AC2+AD2=DC2
∴∠DAC=90°,
∴S四边形ABCD=S△ABC+S△ADC=$\frac{1}{2}$×4×3+$\frac{1}{2}$×5×12=36(米2).
答:这块地的面积是36平方米.
点评 此题主要考查了勾股定理的应用,解答此题的关键是解四边形的问题转化成解三角形的问题再解答.

练习册系列答案
相关题目
12.下列各式中正确的是( )
| A. | $\sqrt{25}$=±5 | B. | $\sqrt{(-3)^{2}}$=-3 | C. | ±$\sqrt{49}$=±7 | D. | $\sqrt{-100}$=10 |
6.在下列运算中,正确的是( )
| A. | (x4)2=x6 | B. | x3•x2=x6 | C. | x2+x2=2x4 | D. | x6÷x2=x4 |
11.冰柜里有四种饮料:2瓶可乐、3瓶咖啡、4瓶桔子水、6瓶汽水,其中可乐和咖啡是含有咖啡因的饮料,那么从冰柜里随机取一瓶饮料,该饮料含有咖啡因的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
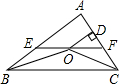 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB与E,交AC于F,过点O作OD⊥AC于D,下列四个结论:其中正确的结论是( )
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB与E,交AC于F,过点O作OD⊥AC于D,下列四个结论:其中正确的结论是( ) 甲乙两人8次射击的成绩如图所示(单位:环)根据图中的信息判断,这8次射击中成绩比较稳定的是甲(填“甲”或“乙”)
甲乙两人8次射击的成绩如图所示(单位:环)根据图中的信息判断,这8次射击中成绩比较稳定的是甲(填“甲”或“乙”)