Question

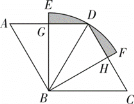
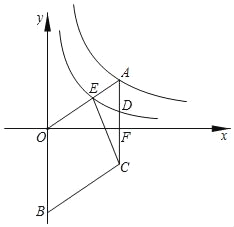
【题目】如图所示，菱形AOBC的顶点B在y轴上，顶点A在反比例函数y＝的图象上，边AC，OA分别交反比例函数y＝的图象于点D，点E，边AC交x轴于点F，连接CE．已知四边形OBCE的面积为12，sin∠AOF＝ ，则k的值为（　　）

A. B. C. D.

Answer 1

【答案】B

【解析】

如图，连接OC，作CH⊥OA于H，EG⊥OF于G．由题意可以假设AF＝3m，OF＝4m，则OA＝OB＝AC＝BC＝5m，构建方程求出m，想办法求出点E坐标即可解决问题．

如图，连接OC，作CH⊥OA于H，EG⊥OF于G．

在Rt△AOF中，∵sin∠AOF＝，

∴可以假设AF＝3m，OF＝4m，则OA＝OB＝AC＝BC＝5m，

∵×3m×4m＝，

∴m＝或﹣（舍弃），

∴OA＝OB＝，OF＝CH＝2，

∵S四边形OBCE＝S△OBC+S△OEC，

∴12＝××2+×OE×2，

∴OE＝，

∵sin∠EOG＝，

∴EG＝，

∴OG＝，

∴E（，），

∵点E在y＝上，

∴k＝，

故选B．