题目内容
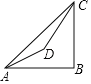
【题目】某风景区内为了方便游客登上山顶，计划从山底A点到山顶C点修建观光缆车，此时从A点观测C点的仰角为45度；施工组经过实地勘察后，为了安全，决定将观光缆车的钢索改为AD、CD两段，D点是半山腰上距离地面AB30米的一个支点，从A点观测D点的仰角为30°．从D点观测山顶C点的仰角为75°，请你通过自己学过的知识来求出这座山的高度BC约为多少米．（结果保留整数．可能用到的数据：
≈1.73．sin75°≈0.96．cos75°≈0.26．tan75°≈3.73）
【答案】60米
【解析】
过D作DE⊥AB于E，DF⊥BC于F，解直角三角形即可得到结论．
解：过D作DE⊥AB于E，DF⊥BC于F，
∴DE＝BF，DF＝BE，
∵∠BAC＝45°，∠B＝90°，
∴AB＝BC，
设AB＝BC＝x，
∵DE＝30，∠DAE＝30°，
∴AE＝
，
∴DF＝BE＝x﹣，CF＝x﹣30，
∵∠CDF＝75°，
∴tan75°＝
＝
＝3.73，
解得：x≈60（m），
答：这座山的高度BC约为60米．
练习册系列答案
天天向上口算本系列答案
相关题目
