Question

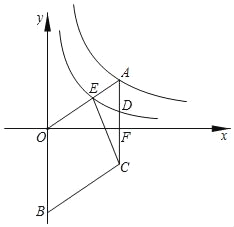
【题目】如图1，已知点，、分别交轴正半轴于点，交轴负半轴于点，且，连接．

（1）若，则_______，此时________．

（2）求的面积．

（3）在线段上取一点使，在上是否存在一点，使得四边形是平行四边形，如果存在，请直接写出点的横坐标，如果不存在，请说明理由．

Answer 1

【答案】（1），9；（2）9；（3）存在，

【解析】

(1)连接PO,根据，可得，再根据，，可得∠OPA=∠OAP=，即可求解．

(2)在（1）的基础上，易得是等腰直角三角形，根据三角形面积公式求解即可．

(3)用待定系数法先求得PO的函数解析式，再求得MN和PA的函数解析式，最后结合MN和PA的解析式解二元一次方程组即可．

解：（1）连接PO

∵

∴

∵，

∴

∴∠OPA=∠OAP=

∴OA=OP=

∴

（2）连接

过点作轴于，轴于

∵

∴，∴

∴点在的角平分线上

∴

∴

∵是的外角

∴

又∵

∴

∴

∴

∴

∵

∴

（3）存在

令，P（-3,3）

解得：

∴

令，M()

解得：

∴

令，,0)

解得：，

∴

∴

解得：