题目内容
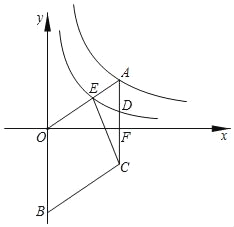
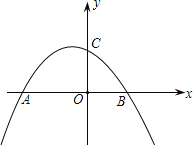
【题目】如图，抛物线
与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C
（1）求点A、B的坐标；
（2）设D为已知抛物线的对称轴上的任意一点，当△ACD的面积等于△ACB的面积时，求点D的坐标；
（3）若直线l过点E（4，0），M为直线l上的动点，当以A、B、M为顶点所作的直角三角形有且只有三个时，求直线l的解析式．
【答案】（1）A（﹣4，0）、B（2，0）；（2）D点坐标为：D1（﹣1，
），D2（﹣1，
）；（3）直线l的解析式为y=
x+3或y=
x﹣3．
【解析】
解：（1）在
中，令y=0，即
，解得x1=﹣4，x2=2．
∵点A在点B的左侧，∴A、B点的坐标为A（﹣4，0）、B（2，0）．
（2）由得，对称轴为x=﹣1．
在中，令x=0，得y=3．
∴OC=3，AB=6，
．
在Rt△AOC中，
．
设△ACD中AC边上的高为h，则有
ACh=9，解得h=
．
如图1，在坐标平面内作直线平行于AC，且到AC的距离=h=，这样的直线有2条，分别是L1和L2，则直线与对称轴x=﹣1的两个交点即为所求的点D．
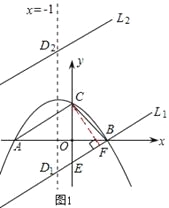
设L1交y轴于E，过C作CF⊥L1于F，则CF=h=，
∴
．
设直线AC的解析式为y=kx+b，
将A（﹣4，0），B（0，3）坐标代入，得
，解得
．
∴直线AC解析式为
．
直线L1可以看做直线AC向下平移CE长度单位（
个长度单位）而形成的，
∴直线L1的解析式为
．
则D1的纵坐标为
．∴D1（﹣1，）．
同理，直线AC向上平移个长度单位得到L2，可求得D2（﹣1，）．
综上所述，D点坐标为：D1（﹣1，），D2（﹣1，）．
（3）如图2，以AB为直径作⊙F，圆心为F．过E点作⊙F的切线，这样的切线有2条．
连接FM，过M作MN⊥x轴于点N．
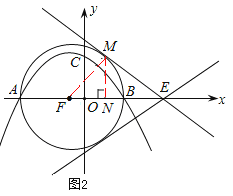
∵A（﹣4，0），B（2，0），∴F（﹣1，0），⊙F半径FM=FB=3．
又FE=5，则在Rt△MEF中，ME=
，sin∠MFE=
，cos∠MFE=
．
在Rt△FMN中，MN=MFsin∠MFE=3×
，FN=MFcos∠MFE=3×
．
则ON=．
∴M点坐标为（，
）．
直线l过M（，），E（4，0），
设直线l的解析式为y=k1x+b1，则有
，解得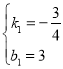
．
∴直线l的解析式为y=x+3．
同理，可以求得另一条切线的解析式为y=x﹣3．
综上所述，直线l的解析式为y=x+3或y=x﹣3．
