题目内容
12. 如图,在等边△ABC中,AB=2,N为AB上一点,且AN=1,∠BAC的平分线交BC于点D,M是AD上的动点,连结BM、MN,则BM+MN的最小值是$\sqrt{3}$.
如图,在等边△ABC中,AB=2,N为AB上一点,且AN=1,∠BAC的平分线交BC于点D,M是AD上的动点,连结BM、MN,则BM+MN的最小值是$\sqrt{3}$.
分析 要求BM+MN的最小值,需考虑通过作辅助线转化BM,MN的值,从而找出其最小值求解.
解答  解:连接CN,与AD交于点M.则CN就是BM+MN的最小值.
解:连接CN,与AD交于点M.则CN就是BM+MN的最小值.
取BN中点E,连接DE.
∵等边△ABC的边长为2,AN=1,
∴BN=AC-AN=2-1=1,
∴BE=EN=AN=1,
又∵AD是BC边上的中线,
∴DE是△BCN的中位线,
∴CN=2DE,CN∥DE,
又∵N为AE的中点,
∴M为AD的中点,
∴MN是△ADE的中位线,
∴DE=2MN,
∴CN=2DE=4MN,
∴CM=$\frac{3}{4}$CN.
在直角△CDM中,CD=$\frac{1}{2}$BC=1,DM=$\frac{1}{2}$AD=$\frac{\sqrt{3}}{2}$,
∴CM=$\sqrt{C{D}^{2}+M{D}^{2}}=\frac{3\sqrt{3}}{4}$,
∴CN=$\frac{4}{3}×\frac{3\sqrt{3}}{4}$=$\sqrt{3}$.
∵BM+MN=CN,
∴BM+MN的最小值为$\sqrt{3}$.
故答案为$\sqrt{3}$
点评 考查等边三角形的性质和轴对称及勾股定理等知识的综合应用,关键是作辅助线转化BM,MN的值解答.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
2.在整式5abc,-7x2+1,-$\frac{2x}{5}$,3.14,$\frac{4x-y}{2}$中,单项式共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |

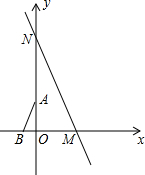 如图,在直角坐标系中,直线y=-$\sqrt{3}x+5\sqrt{3}$分别与x轴、y轴交于点M、N,点A、B分别在y轴、x轴上,且∠B=60°,AB=2,将△ABO绕原点O顺时针转动一周,当AB与直线MN平行时点A的坐标为(-$\frac{3}{2}$,$\frac{\sqrt{3}}{2}$)或($\frac{3}{2}$,-$\frac{\sqrt{3}}{2}$).
如图,在直角坐标系中,直线y=-$\sqrt{3}x+5\sqrt{3}$分别与x轴、y轴交于点M、N,点A、B分别在y轴、x轴上,且∠B=60°,AB=2,将△ABO绕原点O顺时针转动一周,当AB与直线MN平行时点A的坐标为(-$\frac{3}{2}$,$\frac{\sqrt{3}}{2}$)或($\frac{3}{2}$,-$\frac{\sqrt{3}}{2}$). 如图,将一副三角板放在一块,AC与EF所夹的钝角的度数为165°.
如图,将一副三角板放在一块,AC与EF所夹的钝角的度数为165°.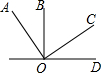 如图,OB⊥OD,OA⊥OC,且∠BOC=58°,则∠AOD的度数为32°.
如图,OB⊥OD,OA⊥OC,且∠BOC=58°,则∠AOD的度数为32°.
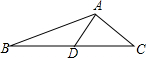 如图△ABC中,点D为BC的中点,AB=5,AC=3,AD=2,则CD长为$\sqrt{13}$.
如图△ABC中,点D为BC的中点,AB=5,AC=3,AD=2,则CD长为$\sqrt{13}$.