题目内容
2.若多项式x2+ax+b分解因式的结果(x-2)(x+3),则a,b的值分别是( )| A. | a=1,b=-6 | B. | a=5,b=6 | C. | a=1,b=6 | D. | a=5,b=-6 |
分析 首先利用多项式乘法将原式展开,进而得出a,b的值,即可得出答案.
解答 解:∵多项式x2+ax+b分解因式的结果为(x-2)(x+3),
∴x2+ax+b=(x-2)(x+3)=x2+x-6,
故a=1,b=-6,
故选:A.
点评 此题主要考查了多项式乘法,正确利用将原式展开是解题关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
14.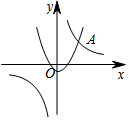 如图,抛物线y=x2+m与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}$+x2+m<0的解集是( )
如图,抛物线y=x2+m与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}$+x2+m<0的解集是( )
 如图,抛物线y=x2+m与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}$+x2+m<0的解集是( )
如图,抛物线y=x2+m与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}$+x2+m<0的解集是( )| A. | x>1 | B. | x<-1 | C. | 0<x<1 | D. | -1<x<0 |
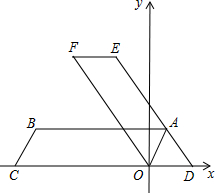 如图,四边形ABCO是平行四边形,OA=2,AB=6,点C在x轴的负半轴上,将?ABCO绕点O顺时针旋转α°(0<α<90°)得到?DEFO,点A的对应点点D恰好落在x轴的正半轴上,且DE经过点A.
如图,四边形ABCO是平行四边形,OA=2,AB=6,点C在x轴的负半轴上,将?ABCO绕点O顺时针旋转α°(0<α<90°)得到?DEFO,点A的对应点点D恰好落在x轴的正半轴上,且DE经过点A.