题目内容
 某健身广场由6个正方形拼成一个长方形(如图),已知中间最小的正方形A的边长是1米,请按要求回答下列问题:
某健身广场由6个正方形拼成一个长方形(如图),已知中间最小的正方形A的边长是1米,请按要求回答下列问题:(1)若设图中最大正方形B的边长是x米,请用含x的代数式分别表示出正方形F、E和C的边长;
(2)观察图形的特点可知,长方形相对的两边是相等的(如图中的MN和PQ),请根据这个等量关系,求出x的值及广场(矩形PQMN)的面积;
(3)现沿着长方形广场的四条边铺设下水管道,由甲、乙2个工程队单独铺设分别需要10天、15天完成.如果两队从同一点开始,沿相反的方向同时施工2天后,因甲队另有任务,余下的工程由乙队单独施工,试问还需要多少天完成?
考点:一元一次方程的应用
专题:几何图形问题
分析:(1)若设图中最大正方形B的边长是x米,最小的正方形的边长是1米,从图中可看出F的边长为(x-1)米,C的边长为
(x+1),E的边长为x-1-1=x-2;
(2)根据长方形相对的两边是相等的(如图中的MN和P Q).根据这个等量关系,求出x的值,再根据长方形的面积公式求解;
(3)根据工作效率×工作时间=工作量这个等量关系且完成工作,工作量就为1,可列方程求解.
| 1 |
| 2 |
(2)根据长方形相对的两边是相等的(如图中的MN和P Q).根据这个等量关系,求出x的值,再根据长方形的面积公式求解;
(3)根据工作效率×工作时间=工作量这个等量关系且完成工作,工作量就为1,可列方程求解.
解答:解:(1)若设图中最大正方形B的边长是x米,最小的正方形的边长是1米.
F的边长为(x-1)米,
C的边长为
(x+1)米,
E的边长为(x-2)米;
(2)∵MQ=PN,
∴x-1+x-2=x+
(x+1),
解得x=7,
矩形PQMN)的面积:
(x+x-1)(x-1+x-2)
=13×11
=143.
故x的值为7,矩形PQMN的面积是143平方米;
(3)设余下的工程由乙队单独施工,还要x天完成.
(
+
)×2+
x=1,
解得x=10.
答:余下的工程由乙队单独施工,还要10天完成.
F的边长为(x-1)米,
C的边长为
| 1 |
| 2 |
E的边长为(x-2)米;
(2)∵MQ=PN,
∴x-1+x-2=x+
| 1 |
| 2 |
解得x=7,
矩形PQMN)的面积:
(x+x-1)(x-1+x-2)
=13×11
=143.
故x的值为7,矩形PQMN的面积是143平方米;
(3)设余下的工程由乙队单独施工,还要x天完成.
(
| 1 |
| 10 |
| 1 |
| 15 |
| 1 |
| 15 |
解得x=10.
答:余下的工程由乙队单独施工,还要10天完成.
点评:本题考查一元一次方程的应用,理解题意能力和看图的能力,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
相关题目
2011年12月,天文学家发现一颗新的与地球最近的系外类地行星,名为“HD85512B”,距地球大约36光年,此距离用科学记数法表示为( )(1光年=30万千米)
| A、108×108m |
| B、1.08×1010m |
| C、3×108m |
| D、108×108km |
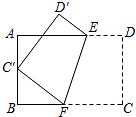 如图所示,将矩形ABCD沿直线EF折叠,使顶点C恰好落在AB边的中点C′上,若AB=6,BC=9,则BF的长为( )
如图所示,将矩形ABCD沿直线EF折叠,使顶点C恰好落在AB边的中点C′上,若AB=6,BC=9,则BF的长为( )| A、4 | ||
B、3
| ||
| C、4.5 | ||
D、2
|
线段AB被分为2:3:4三部分,已知第一部分和第三部分的中点间的距离是6.6cm,则线段AB的长为( )
| A、8.9cm |
| B、9.9cm |
| C、10.8cm |
| D、11.7cm |
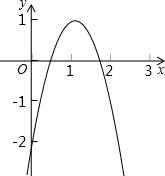 如图2,已知二次函数y=ax2+bx+c的图象与x轴相交于(x1,0 ),(x2,0)两点,且0<x1<1,1<x2<2,与y轴相交于(O,-2),下列结论:①2a+b>1;②3a+b>0;③a+b<2; ④b2+8a>0;⑤a-b>2. 其中正确结论的个数为 ( )
如图2,已知二次函数y=ax2+bx+c的图象与x轴相交于(x1,0 ),(x2,0)两点,且0<x1<1,1<x2<2,与y轴相交于(O,-2),下列结论:①2a+b>1;②3a+b>0;③a+b<2; ④b2+8a>0;⑤a-b>2. 其中正确结论的个数为 ( )