题目内容
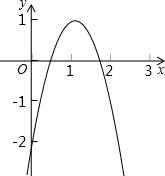 如图2,已知二次函数y=ax2+bx+c的图象与x轴相交于(x1,0 ),(x2,0)两点,且0<x1<1,1<x2<2,与y轴相交于(O,-2),下列结论:①2a+b>1;②3a+b>0;③a+b<2; ④b2+8a>0;⑤a-b>2. 其中正确结论的个数为 ( )
如图2,已知二次函数y=ax2+bx+c的图象与x轴相交于(x1,0 ),(x2,0)两点,且0<x1<1,1<x2<2,与y轴相交于(O,-2),下列结论:①2a+b>1;②3a+b>0;③a+b<2; ④b2+8a>0;⑤a-b>2. 其中正确结论的个数为 ( )| A、1个 | B、2个 | C、3个 | D、4个 |
考点:二次函数图象与系数的关系
专题:
分析:由抛物线的开口方向判断a的符号,由抛物线与y轴的交点判断c的符号,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答:解:由图知:c=-2.
当x=1时,a+b-2>0,所以a+b>2,故③错误;
因为抛物线与x轴有两个交点,所b2-4ac>0即b2+8a>0,所以④正确;
当x=2时,由图象得y=4a+2b+c<0,即4a+2b-2<0,所以4a+2b<1,故①错误;
因为4a+2b-2<0,又a+b-2>0,所以3a+b<0,故②错;
当x=-1时a-b+c<0,即a-b-2<0,所以a-b<2故⑤错误.
故选:A.
当x=1时,a+b-2>0,所以a+b>2,故③错误;
因为抛物线与x轴有两个交点,所b2-4ac>0即b2+8a>0,所以④正确;
当x=2时,由图象得y=4a+2b+c<0,即4a+2b-2<0,所以4a+2b<1,故①错误;
因为4a+2b-2<0,又a+b-2>0,所以3a+b<0,故②错;
当x=-1时a-b+c<0,即a-b-2<0,所以a-b<2故⑤错误.
故选:A.
点评:考查二次函数y=ax2+bx+c系数符号的确定由抛物线开口方向、对称轴和抛物线与坐标轴的交点确定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若n是正整数,则下列各式中正确的是( )
| A、(-a)n=-an |
| B、(-a2n+1)=a2n+1 |
| C、(-a)2n=-a2n |
| D、(-a)2n-1=-a2n-1 |
-24表示( )
| A、4个-2相乘 |
| B、4个2相乘 |
| C、2个4相乘的相反数 |
| D、4个2相乘的相反数 |
下列运算中正确的是( )
| A、2a+3b=5ab | ||
B、3a-2=
| ||
C、(-sin30°)0=-
| ||
| D、(-x5)(-x)3=x8 |
 某健身广场由6个正方形拼成一个长方形(如图),已知中间最小的正方形A的边长是1米,请按要求回答下列问题:
某健身广场由6个正方形拼成一个长方形(如图),已知中间最小的正方形A的边长是1米,请按要求回答下列问题: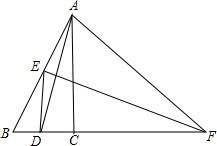 如图,已知AD是∠BAC的角平分线,AD的垂直平分线EF交AB于点E,交BC延长线于F.求证:
如图,已知AD是∠BAC的角平分线,AD的垂直平分线EF交AB于点E,交BC延长线于F.求证: 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,对称轴是直线x=1.①b2>4ac;②4a-2b+c<0;③不等式ax2+bx+c>0的解集是x≥3.5;④若(-2,y1),(5,y2)是抛物线上的两点,则y1<y2.上述四个判断中正确的是
如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,对称轴是直线x=1.①b2>4ac;②4a-2b+c<0;③不等式ax2+bx+c>0的解集是x≥3.5;④若(-2,y1),(5,y2)是抛物线上的两点,则y1<y2.上述四个判断中正确的是 有一条直的等宽纸带,按如图折叠时,纸带重叠部分中∠α=
有一条直的等宽纸带,按如图折叠时,纸带重叠部分中∠α=