题目内容
线段AB被分为2：3：4三部分，已知第一部分和第三部分的中点间的距离是6.6cm，则线段AB的长为（ ）
| A、8.9cm |
| B、9.9cm |
| C、10.8cm |
| D、11.7cm |
考点：两点间的距离
专题：
分析：根据线段间的比例，可设出未知数，根据线段中点的性质，可得EC、DF的长，根据线段的和差，可得关于x的方程，根据线段的和差，可得答案．
解答：解：如图：
，
设AC=2x，CD=3x，DB=4x，
由线段中点的性质，得
EC=x，DF=2x，
由线段的和差，得
EF=EC+CD+DF=x+3x+2x=6.6cm，
解得x=1.1cm．
由线段的和差，得AB=AC+CD+DB=2x+3x+4x=9x=9×1.1=9.9cm．
故选：B．
，设AC=2x，CD=3x，DB=4x，
由线段中点的性质，得
EC=x，DF=2x，
由线段的和差，得
EF=EC+CD+DF=x+3x+2x=6.6cm，
解得x=1.1cm．
由线段的和差，得AB=AC+CD+DB=2x+3x+4x=9x=9×1.1=9.9cm．
故选：B．
点评：本题考查了两点间的距离，利用线段间的比设出未知数，利用线段的和差得出方程是解题关键．
练习册系列答案
相关题目
某健身广场由6个正方形拼成一个长方形（如图），已知中间最小的正方形A的边长是1米，请按要求回答下列问题：
在边长为1的小正方形组成的正方形网格中建立如图片所示的平面直角坐标系，已知格点三角形ABC（三角形的三个顶点都在小正方形上）
如图，在?ABCD中，AB=6cm，点P从点A出发，以1cm/s的速度向点B运动，点Q从点C出发，以2cm/s的速度向点D运动，当一个点运动到端点时，另一个点也停止运动，经过多长时间后，四边形APQD是平行四边形？若n是正整数，则下列各式中正确的是（ ）
| A、（-a）n=-an |
| B、（-a2n+1）=a2n+1 |
| C、（-a）2n=-a2n |
| D、（-a）2n-1=-a2n-1 |
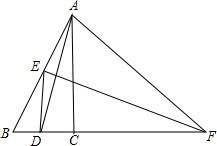如图，已知AD是∠BAC的角平分线，AD的垂直平分线EF交AB于点E，交BC延长线于F．求证：
有一条直的等宽纸带，按如图折叠时，纸带重叠部分中∠α=