题目内容
20.计算:$\sqrt{12}$-4$\sqrt{\frac{1}{2}}$-tan60°+|$\sqrt{3}$-2|.分析 原式前两项化为最简二次根式,第三项利用特殊角的三角函数值计算,最后一项利用绝对值的代数意义化简,计算即可得到结果.
解答 解:原式=2$\sqrt{3}$-4×$\frac{\sqrt{2}}{2}$-$\sqrt{3}$+2-$\sqrt{3}$
=2-2$\sqrt{2}$.
点评 此题考查了实数的运算,以及特殊角的三角函数值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
11.已知数的大小比较:①-1>0;②-1<0;③-1>-2;④-1<-2.其中正确的有( )
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
5.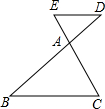 如图,已知点D、E分别在△ABC的边BA、CA的延长上,下列给出的条件中,不能判定DE∥BC的是( )
如图,已知点D、E分别在△ABC的边BA、CA的延长上,下列给出的条件中,不能判定DE∥BC的是( )
 如图,已知点D、E分别在△ABC的边BA、CA的延长上,下列给出的条件中,不能判定DE∥BC的是( )
如图,已知点D、E分别在△ABC的边BA、CA的延长上,下列给出的条件中,不能判定DE∥BC的是( )| A. | BD:AB=CE:AC | B. | DE:BC=AB:AD | C. | AB:AC=AD:AE | D. | AD:DB=AE:EC |
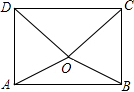 如图,O为矩形ABCD内的一点,满足OD=OC,若O点到边AB的距离为d,到边DC的距离为3d,且OB=2d,求该矩形对角线的长2$\sqrt{7}$d.
如图,O为矩形ABCD内的一点,满足OD=OC,若O点到边AB的距离为d,到边DC的距离为3d,且OB=2d,求该矩形对角线的长2$\sqrt{7}$d.

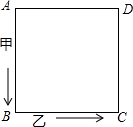 如图,两人沿着边长为70米的正方形,按A→B→C→D→A…的方向行走.甲从A点以65米/分的速度、乙从B点以72米/分的速度行走,甲、乙两人同时出发,当乙第一次追上甲时,将在正方形的AD边上.
如图,两人沿着边长为70米的正方形,按A→B→C→D→A…的方向行走.甲从A点以65米/分的速度、乙从B点以72米/分的速度行走,甲、乙两人同时出发,当乙第一次追上甲时,将在正方形的AD边上. 等边△ABC高为7$\sqrt{3}$,边长为14.BD为AC边上高,P是BD上的动点,且E是BC上-点,BE=CE,则△PEC的周长最小值为7$\sqrt{3}$+7.
等边△ABC高为7$\sqrt{3}$,边长为14.BD为AC边上高,P是BD上的动点,且E是BC上-点,BE=CE,则△PEC的周长最小值为7$\sqrt{3}$+7.