题目内容
15.甲车和乙车从A、B两地同时出发,沿同一线路相向匀速行驶,出发后1.5h两车相遇,相遇时甲车比乙车少走30km,相遇后1.2h乙车到达A地.(1)两车的行驶速度分别是多少?
(2)相遇后,若乙车速度不变,甲车想和乙车同时到达目的地,那么甲车要比原来的行驶速度增加多少km/h?
(3)相遇后,甲车到B地间的部分路段限速120km/h,部分路段限速140km/h,(2)中甲车在相应路段,既不超速又不低于限速行驶,刚好能和乙车同时到达目的地,试求限速120km/h和限速140km/h的路段各多少km?
分析 (1)利用1.5h两车相遇,相遇时甲车比乙车少走30km,进而得出等式求出答案;
(2)利用相遇后甲车行驶的距离等于乙相遇前行驶的距离,进而得出等式求出答案;
(3)利用行驶剩余距离的时间为1.2小时,进而得出等式求出答案.
解答 (1)解:设乙车速度为vkm/h,依题意有
1.2v=1.5v-30,
解得:v=100,
则甲车的速度为:$\frac{1.5v-30}{1.5}$,
即$\frac{1.5×100-30}{1.5}=80$.
答:乙的速度为:100km/h,甲的速度为:80km/h;
(2)设甲车的行驶速度比原来增加akm/h,则有:
(80+a)×1.2=100×1.5,
解得:a=45.
答:甲车要比原来的行驶速度增加45km/h;
(3)设限速120km/h的路段长xkm,则限速140km/h的路段长(150-x)km,
则依题意有$\frac{x}{120}+\frac{150-x}{140}=1.2$,
解得:x=108,150-x=42.
答:限速120km/h路段长108km,限速140km/h的路段42km.
点评 此题主要考查了一元一次方程的应用,根据题意正确结合形式的路程与时间得出等式是解题关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
4.一件商品按标价的九折出售可获利20%,若商品的标价为a元,进价为b元,则可列方程( )
| A. | 0.9a-b=20%•b | B. | 0.9a+b=20%•b | C. | 0.9a-b=20% | D. | a-b=20% |
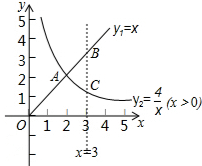 如图所示,函数y1=x(x>0),y2=$\frac{4}{x}$(x>0)的图象交于点A,与直线x=3分别交于B,C两点,给出以下四个结论:
如图所示,函数y1=x(x>0),y2=$\frac{4}{x}$(x>0)的图象交于点A,与直线x=3分别交于B,C两点,给出以下四个结论: 如图,在△ABC中,DE∥BC,当△ADE与△ABC的周长比为1:3时,那么DE:BC=1:3.
如图,在△ABC中,DE∥BC,当△ADE与△ABC的周长比为1:3时,那么DE:BC=1:3.