题目内容
9.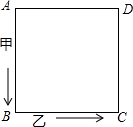 如图,两人沿着边长为70米的正方形,按A→B→C→D→A…的方向行走.甲从A点以65米/分的速度、乙从B点以72米/分的速度行走,甲、乙两人同时出发,当乙第一次追上甲时,将在正方形的AD边上.
如图,两人沿着边长为70米的正方形,按A→B→C→D→A…的方向行走.甲从A点以65米/分的速度、乙从B点以72米/分的速度行走,甲、乙两人同时出发,当乙第一次追上甲时,将在正方形的AD边上.
分析 设乙x分钟后追上甲,根据乙追上甲时,比甲多走了70×3=210米,可得出方程,求出时间后,计算乙所走的路程,继而可判断在哪一条边上相遇.
解答 解:(1)设乙第一次追上甲用了x分钟,
由题意得:72x-65x=70×3,
解得:x=30,
而72×30=2160=70×30+60,
30÷4=7…2,
所以乙走到D点,再走60米即可追上甲,即在AD边上.
答:乙第一次追上甲是在AD边上.
故答案为:AD.
点评 此题考查一元一次方程的实际运用,掌握行程问题中追击问题的基本数量关系是解决问题的关键.

练习册系列答案
相关题目
4.一件商品按标价的九折出售可获利20%,若商品的标价为a元,进价为b元,则可列方程( )
| A. | 0.9a-b=20%•b | B. | 0.9a+b=20%•b | C. | 0.9a-b=20% | D. | a-b=20% |
13. 如图,数轴上点P表示的数可能是( )
如图,数轴上点P表示的数可能是( )
 如图,数轴上点P表示的数可能是( )
如图,数轴上点P表示的数可能是( )| A. | $-\sqrt{5}$ | B. | $\sqrt{5}$ | C. | -3.8 | D. | $-\sqrt{10}$ |
20.请估计$\sqrt{10}-1$的值在( )
| A. | 1与2之间 | B. | 2与3之间 | C. | 3与4之间 | D. | 4与5之间 |
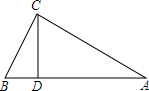 如图,△ABC中,∠C=90°,若CD⊥AB于D,且BD=4,AD=9,则CD=6.
如图,△ABC中,∠C=90°,若CD⊥AB于D,且BD=4,AD=9,则CD=6.