题目内容
⊙O的半径OA=10cm,弦AB=8cm,P为弦AB上一动点,则点P到圆心O的最短距离为 cm.
考点:垂径定理,勾股定理
专题:
分析:过点O作OD⊥AB于点D,根据垂径定理求出AD的长,再由勾股定理求出OD的长,故可得出结论.
解答: 解:过点O作OD⊥AB于点D,则点P与点D垂直时点P到圆心O的距离最短,
解:过点O作OD⊥AB于点D,则点P与点D垂直时点P到圆心O的距离最短,
∵OD⊥AB,AB=8cm,
∴AD=
AB=
×8=4cm,
在Rt△AOD中,
∵OA=10cm,AD=4cm,
∴OD=
=
=2
,
∴点P到圆心O的最短距离为2
.
故答案为:2
.
 解:过点O作OD⊥AB于点D,则点P与点D垂直时点P到圆心O的距离最短,
解:过点O作OD⊥AB于点D,则点P与点D垂直时点P到圆心O的距离最短,∵OD⊥AB,AB=8cm,
∴AD=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△AOD中,
∵OA=10cm,AD=4cm,
∴OD=
| OA2-AD2 |
| 102-42 |
| 21 |
∴点P到圆心O的最短距离为2
| 21 |
故答案为:2
| 21 |
点评:本题考查的是勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
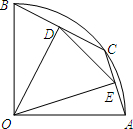 如图,在半径为2的扇形OAB中,∠AOB=90°,点C是
如图,在半径为2的扇形OAB中,∠AOB=90°,点C是
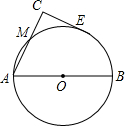 如图,AB为⊙O的直径,CE与⊙O相切于E,AC⊥CE于C,AC交⊙O于M,若AM=2CM=2,求CE的长.
如图,AB为⊙O的直径,CE与⊙O相切于E,AC⊥CE于C,AC交⊙O于M,若AM=2CM=2,求CE的长. 如图是抛物线y=ax2+bx+c的图象的一部分,请你根据图象写出方程ax2+bx+c=0的两根是
如图是抛物线y=ax2+bx+c的图象的一部分,请你根据图象写出方程ax2+bx+c=0的两根是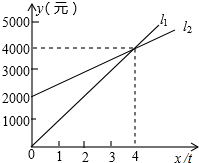 如图,l1反映了某公司产品的销售收入与销售量的关系,l2反映了该公司产品的销售成本与销售量的关系,根据图象填空:
如图,l1反映了某公司产品的销售收入与销售量的关系,l2反映了该公司产品的销售成本与销售量的关系,根据图象填空: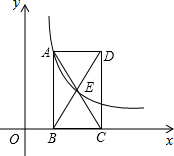 如图,已知点A(1,3)在函数y=
如图,已知点A(1,3)在函数y=