题目内容
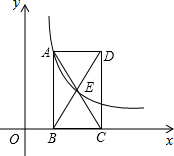 如图,已知点A(1,3)在函数y=
如图,已知点A(1,3)在函数y=| k |
| x |
(1)求k的值;
(2)当∠ABD=45°时,求点C的坐标;
(3)当∠ABD=45°时,求直线BD的解析式.
考点:反比例函数综合题
专题:综合题
分析:(1)只需把点A的坐标代入反比例函数的解析式就可求出k的值.
(2)由∠ABD=45°可证得矩形ABCD是正方形,由A(1,3)可求出OC长,就可解决问题.
(3)由(2)可得OB、OC、DC长,从而得到点B、D的坐标,然后运用待定系数法就可求出直线BD的解析式.
(2)由∠ABD=45°可证得矩形ABCD是正方形,由A(1,3)可求出OC长,就可解决问题.
(3)由(2)可得OB、OC、DC长,从而得到点B、D的坐标,然后运用待定系数法就可求出直线BD的解析式.
解答:解:(1)∵点A(1,3)在函数y=
(x>0)的图象上,
∴k=1×3=3.
∴k的值为3.
(2)∵四边形ABCD是矩形,
∴∠BAD=90°.
∵∠ABD=45°,
∴∠ADB=45°=∠ABD,
∴AD=AB,
∴矩形ABCD是正方形,
∴DC=BC=AB.
∵点A的坐标为(1,3),
∴OB=1,DC=BC=AB=3,
∴OC=4,∴点C的坐标为(4,0).
(3)由(2)得:OB=1,0C=4,DC=3,
则点B的坐标为(1,0),点D的坐标为(4,3).
设直线BD的解析式为y=mx+n,
则有
,
解得:
.
故直线BD的解析式为y=x-1.
| k |
| x |
∴k=1×3=3.
∴k的值为3.
(2)∵四边形ABCD是矩形,
∴∠BAD=90°.
∵∠ABD=45°,
∴∠ADB=45°=∠ABD,
∴AD=AB,
∴矩形ABCD是正方形,
∴DC=BC=AB.
∵点A的坐标为(1,3),
∴OB=1,DC=BC=AB=3,
∴OC=4,∴点C的坐标为(4,0).
(3)由(2)得:OB=1,0C=4,DC=3,
则点B的坐标为(1,0),点D的坐标为(4,3).
设直线BD的解析式为y=mx+n,
则有
|
解得:
|
故直线BD的解析式为y=x-1.
点评:本题主要考查了运用待定系数法求反比例函数及一次函数的解析式、正方形的判定与性质等知识,运用待定系数法是解决本题的关键.

练习册系列答案
相关题目
用一个平面去截一个几何体,得到的截面是三角形,这个几何体可能是( )
| A、圆锥 | B、圆柱 |
| C、球体 | D、以上都有可能 |
 如图,已知抛物线y=x2+bx+c与x轴交于A、B两点,交y轴负半轴于C点,若∠ACB=90°,且
如图,已知抛物线y=x2+bx+c与x轴交于A、B两点,交y轴负半轴于C点,若∠ACB=90°,且 如图,在Rt△ABC中,AB=AC,点D为BC的中点,∠MDN=90°,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.下列结论:①(BE+CF)=
如图,在Rt△ABC中,AB=AC,点D为BC的中点,∠MDN=90°,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.下列结论:①(BE+CF)= (1)数轴上表示下列有理数:-1,1
(1)数轴上表示下列有理数:-1,1