题目内容
某商品的进价为每件50元,售价为每件60元,每天可卖出190件;如果每件商品的售价每上涨1元,则每天少卖10件,设每件商品的售价上涨x元(x为正整数),每天的销售利润为y元.
(1)求y关于x的关系式;
(2)每件商品的售价定为多少元时,每天的利润恰为1980元?
(3)每件商品的售价定为多少元时,每天可获得最大利润?最大利润是多少元?
(1)求y关于x的关系式;
(2)每件商品的售价定为多少元时,每天的利润恰为1980元?
(3)每件商品的售价定为多少元时,每天可获得最大利润?最大利润是多少元?
考点:二次函数的应用,一元二次方程的应用
专题:
分析:(1)利用销量乘以每件利润=总利润得出关系式即可;
(2)利用(1)中所求关系式,进而使y=1980进而得出即可;
(3)利用配方法求出二次函数最值,结合x的取值范围得出答案.
(2)利用(1)中所求关系式,进而使y=1980进而得出即可;
(3)利用配方法求出二次函数最值,结合x的取值范围得出答案.
解答:解:(1)设每件商品的售价上涨x元(x为正整数),每天的销售利润为y元,
则y=(60-50+x)(190-10x)=-10x2+90x+1900;
(2)当y=1980,则1980=-10x2+90x+1900,
解得:x1=1,x2=8.
故每件商品的售价定为61元或68元时,每天的利润恰为1980元;
(3)y=-10x2+90x+1900=-10(x-
)2+2102.5,
故当x=5或4时,y=2100(元),
即每件商品的售价定为64元或65元时,每天可获得最大利润,最大利润是2100元.
则y=(60-50+x)(190-10x)=-10x2+90x+1900;
(2)当y=1980,则1980=-10x2+90x+1900,
解得:x1=1,x2=8.
故每件商品的售价定为61元或68元时,每天的利润恰为1980元;
(3)y=-10x2+90x+1900=-10(x-
| 9 |
| 2 |
故当x=5或4时,y=2100(元),
即每件商品的售价定为64元或65元时,每天可获得最大利润,最大利润是2100元.
点评:此题主要考查了二次函数的应用以及一元二次方程的解法,得出y与x的函数关系式是解题关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
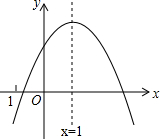 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中:①ac>0;②2a+b=0;③b2-4ac>0;④a-b+c>0.正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中:①ac>0;②2a+b=0;③b2-4ac>0;④a-b+c>0.正确的是( )| A、①② | B、②③ |
| C、②③④ | D、①②③④ |
甲站到乙站另有8个中间停靠站,共需准备( )种动车票.
| A、90 | B、56 | C、45 | D、28 |
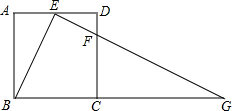 如图,在正方形ABCD中,E,F分别是边AD,CD上的点,AE=ED,DF=
如图,在正方形ABCD中,E,F分别是边AD,CD上的点,AE=ED,DF=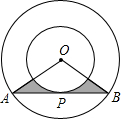 如图,两同心圆的圆心为O,半径分别为6,3,大圆的弦AB切小圆于P,则图中阴影部分的周长是
如图,两同心圆的圆心为O,半径分别为6,3,大圆的弦AB切小圆于P,则图中阴影部分的周长是 已知AE∥BF,AE=BF,AC=BD.求证:ED=FC.
已知AE∥BF,AE=BF,AC=BD.求证:ED=FC.