题目内容
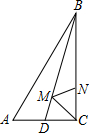 如图△ABC,∠ACB=90°,BC=12,AC=5,AB=13,BD平分∠ABC,M、N分别为BD、BC上的点,则CM+MN的最小值是
如图△ABC,∠ACB=90°,BC=12,AC=5,AB=13,BD平分∠ABC,M、N分别为BD、BC上的点,则CM+MN的最小值是考点:轴对称-最短路线问题
专题:
分析:过点C作CE⊥AB于点E,交BD于点M,过点M作MN⊥BC于N,则CE即为CM+MN的最小值,再根据三角形的面积公式求出CE的长,即为CM+MN的最小值.
解答: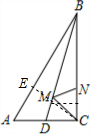 解:过点C作CE⊥AB于点E,交BD于点M,过点M作MN⊥BC于N,
解:过点C作CE⊥AB于点E,交BD于点M,过点M作MN⊥BC于N,
∵BD平分∠ABC,ME⊥AB于点E,MN⊥BC于N,
∴MN=ME,
∴CE=CM+ME=CM+MN的最小值.
∵,∠ACB=90°,BC=12,AC=5,AB=13,
∴
AB•CE=
BC•AC,
即13CE=12×5
∴CE=
.
即CM+MN的最小值为
.
故答案为
.
 解:过点C作CE⊥AB于点E,交BD于点M,过点M作MN⊥BC于N,
解:过点C作CE⊥AB于点E,交BD于点M,过点M作MN⊥BC于N,∵BD平分∠ABC,ME⊥AB于点E,MN⊥BC于N,
∴MN=ME,
∴CE=CM+ME=CM+MN的最小值.
∵,∠ACB=90°,BC=12,AC=5,AB=13,
∴
| 1 |
| 2 |
| 1 |
| 2 |
即13CE=12×5
∴CE=
| 60 |
| 13 |
即CM+MN的最小值为
| 60 |
| 13 |
故答案为
| 60 |
| 13 |
点评:本题考查了轴对称-最短路线问题,关键是画出符合条件的图形,题目具有一定的代表性,是一道比较好的题目.

练习册系列答案
相关题目
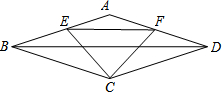 如图,菱形ABCD中,点E,F分别是边AB,AD的中点,连接CE,CF,EF,若四边形ABCD的面积是40cm2,则△CEF的面积为( )
如图,菱形ABCD中,点E,F分别是边AB,AD的中点,连接CE,CF,EF,若四边形ABCD的面积是40cm2,则△CEF的面积为( )| A、5cm2 |
| B、10cm2 |
| C、15cm2 |
| D、20cm2 |
 C为等腰△ABE一腰AB延长线上一点且BC=EF,C,D,F三点共线,求证:CD=DF.
C为等腰△ABE一腰AB延长线上一点且BC=EF,C,D,F三点共线,求证:CD=DF.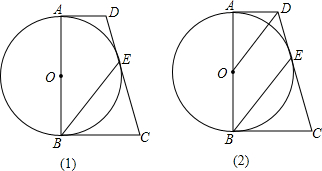
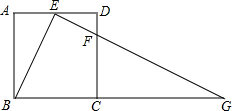 如图,在正方形ABCD中,E,F分别是边AD,CD上的点,AE=ED,DF=
如图,在正方形ABCD中,E,F分别是边AD,CD上的点,AE=ED,DF=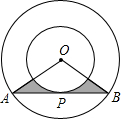 如图,两同心圆的圆心为O,半径分别为6,3,大圆的弦AB切小圆于P,则图中阴影部分的周长是
如图,两同心圆的圆心为O,半径分别为6,3,大圆的弦AB切小圆于P,则图中阴影部分的周长是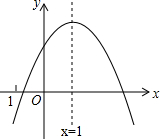 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中:①ac>0;②2a+b=0;③b2-4ac>0;④a-b+c>0.正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中:①ac>0;②2a+b=0;③b2-4ac>0;④a-b+c>0.正确的是( )