题目内容
12. 某校数学兴趣小组在探究如何求tan 15°,cos15°的值,经过自主思考、合作交流讨论,得到以下思路:
某校数学兴趣小组在探究如何求tan 15°,cos15°的值,经过自主思考、合作交流讨论,得到以下思路:思路一 如图1,在Rt△ABC中,∠C=90°,∠ABC=30°,延长CB至点D,使BD=BA,连接AD.设AC=1,则BD=BA=2,BC=$\sqrt{3}$.
tanD=tan15°=$\frac{1}{2+\sqrt{3}}$=$\frac{2-\sqrt{3}}{(2+\sqrt{3})(2-\sqrt{3})}$=2-$\sqrt{3}$.
思路二 利用科普书上的有关公式:
tan(α±β)=$\frac{tanα+tanβ}{1±tanα•tanβ}$;
cos(α±β)=cosαcosβ±sinαsinβ.
例如α=60°,β=45°代入差角正切公式:
tan15°=tan(60°-45°)=$\frac{tan60°-tan45°}{1+tan60°•tan45°}$=$\frac{\sqrt{3}-1}{1+\sqrt{3}}$=2-$\sqrt{3}$.
思路三 在顶角为30°的等腰三角形中,作腰上的高也可以…
思路四 …
请解决下列问题(上述思路仅供参考).
(1)类比:求出tan75°的值和cos15°的值;
(2)应用:如图2,某县要在宽为10米的幸福大道两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成105°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,求路灯的灯柱BC高度.
(精确到0.1米,参考数据$\sqrt{6}$≈2.449,$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
分析 (1)根据思路二直接套用公式计算即可;
(2)作DE⊥AB于点E,CF⊥DE于点F,可得矩形BCFE,进而可得∠ODE=15°、∠DOE=75°,在RT△CDF中根据三角函数分别求出DF、CF=BE的长,在RT△ODE中求出DE的长,由BC=EF=DE-DF可得答案.
解答 解:(1)tan75°=tan(45°+30°)=$\frac{tan45°+tan30°}{1-tan45°•tan30°}$=$\frac{1+\frac{\sqrt{3}}{3}}{1-\frac{\sqrt{3}}{3}}$=2+$\sqrt{3}$;
cos15°=cos(60°-45°)=cos60°cos45°+sin60°sin45°=$\frac{1}{2}$×$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{3}}{2}$×$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{6}+\sqrt{2}}{4}$;
(2)如图2,作DE⊥AB于点E,CF⊥DE于点F,
∵BC⊥AB,
∴∠ABC=∠BEF=∠FEC=90°,
∴四边形BEFC是矩形,
∴∠FCB=90°,BC=EF,BE=CF,
∵DO⊥CD,
∴∠ODC=90°,
∴∠DOE+∠DOE=∠ODE+∠CDF=∠CDF+∠DCF=90°,
∴∠ODE=∠DCF=∠DCB-∠FCB=105°-90°=15°,
∠DOE=∠CDF=90°-15°=75°,
∵cos15°=$\frac{\sqrt{6}+\sqrt{2}}{4}$≈0.966,tan75°=2+$\sqrt{3}$≈3.732,
在RT△CDF中,CD=2米,
∴CF=DC•cos15°≈2×0.966=1.932米,
∵OE=OB-BE=0B-CF=5-1.932=3.068米,
∴DE=OE•tan75°=3.068×3.732=11.450米,
DF=CFtan75°=0.573,
∴BC=EF=DE-DF=11.450-0.573≈11(米),
答:此时路灯的灯柱BC的高度大约11米.
点评 本题考查了相似三角形的性质,直角三角形的性质,锐角三角函数的概念,正确的作出辅助线构造相似三角形是解题的关键.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案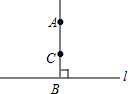 如图所示,因为AB⊥l,BC⊥l,B为垂足,所以AB和BC重合,其理由是( )
如图所示,因为AB⊥l,BC⊥l,B为垂足,所以AB和BC重合,其理由是( )| A. | 两点确定一条直线 | |
| B. | 在同一平面内,过一点有且只有一条直线与已知直线垂直 | |
| C. | 过一点能作一条垂线 | |
| D. | 垂线段最短 |
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $-\frac{3}{2}$ |
| A. | 7 | B. | 4 | C. | ±$\sqrt{3}$ | D. | ±3 |
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
 如图是一个正方体的表面展开图,则原正方体标有数字“1”所在面的对面标有数字( )
如图是一个正方体的表面展开图,则原正方体标有数字“1”所在面的对面标有数字( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |