题目内容
11.图1是一种可折叠台灯,它放置在水平桌面上,将其抽象成图2,其中点B,E,D均为可转动点.现测得AB=BE=ED=CD=15cm,经多次调试发现当点B,E所在直线垂直经过CD的中点F时(如图3所示)放置较平稳.(1)求平稳放置时灯座DC与灯杆DE的夹角的大小;
(2)为保护视力,写字时眼睛离桌面的距离应保持在30cm,为防止台灯刺眼,点A离桌面的距离应不超过30cm,求台灯平稳放置时∠ABE的最大值.(结果精确到0.01°,参考数据:$\sqrt{3}$≈1.732,sin7.70°≈0.134,cos82.30°≈0.134,可使用科学计算器)

分析 (1)由题意得:DF=$\frac{1}{2}$CD=$\frac{15}{2}$cm,EF⊥CD,根据三角函数的定义即可得到结论;
(2)如图3,过A作AH⊥BE交EB的延长线于H,求得EF=15×$\frac{\sqrt{3}}{2}$=$\frac{15\sqrt{3}}{2}$,根据cos∠ABH=$\frac{BH}{AB}$≈0.134,根据得到结论.
解答 解:(1)由题意得:DF=$\frac{1}{2}$CD=$\frac{15}{2}$cm,EF⊥CD,
∴cosD=$\frac{DF}{DE}=\frac{1}{2}$,
∴∠D=60°;
答:平稳放置时灯座DC与灯杆DE的夹角是60°;
(2)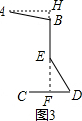 如图3,过A作AH⊥BE交EB的延长线于H,
如图3,过A作AH⊥BE交EB的延长线于H,
∴HF=30,
∵EF=15×$\frac{\sqrt{3}}{2}$=$\frac{15\sqrt{3}}{2}$,
∴BH=30-BE-EF=15-$\frac{15\sqrt{3}}{2}$,
∴cos∠ABH=$\frac{BH}{AB}$≈0.134,
∴∠ABH≈82.30°,
∴∠ABE=97.70°.
答:台灯平稳放置时∠ABE的最大值是97.70°.
点评 此题主要考查了解直角三角形的应用,充分体现了数学与实际生活的密切联系,解题的关键是表示出线段的长后,理清线段之间的关系.

练习册系列答案
相关题目
1.如果一个角的补角是130°,那么这个角的余角的度数是( )
| A. | 30° | B. | 40° | C. | 50° | D. | 90° |
2.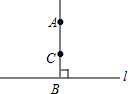 如图所示,因为AB⊥l,BC⊥l,B为垂足,所以AB和BC重合,其理由是( )
如图所示,因为AB⊥l,BC⊥l,B为垂足,所以AB和BC重合,其理由是( )
 如图所示,因为AB⊥l,BC⊥l,B为垂足,所以AB和BC重合,其理由是( )
如图所示,因为AB⊥l,BC⊥l,B为垂足,所以AB和BC重合,其理由是( )| A. | 两点确定一条直线 | |
| B. | 在同一平面内,过一点有且只有一条直线与已知直线垂直 | |
| C. | 过一点能作一条垂线 | |
| D. | 垂线段最短 |
3.计算-$\frac{1}{2}$-1的结果等于( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $-\frac{3}{2}$ |
20.已知a+$\frac{1}{a}$=$\sqrt{7}$,则a-$\frac{1}{a}$的值为( )
| A. | 7 | B. | 4 | C. | ±$\sqrt{3}$ | D. | ±3 |
 如图,在四边形ABCD中,AD∥BC,AD=8,BC=16,点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动,点P停止运动时,点Q也随之停止运动,设运动时间为t秒.
如图,在四边形ABCD中,AD∥BC,AD=8,BC=16,点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动,点P停止运动时,点Q也随之停止运动,设运动时间为t秒.