题目内容
平面内两条直线AB、CD互相平行,在两直线外取一点P(如图),

(1)如图(1),请直接写出∠A,∠P,∠C之间存在的等量关系(不写理由);
(2)如图(2),写出∠A,∠P,∠C之间存在的等量关系,并说明理由;
(3)如图(3),请直接写出∠A,∠P,∠C之间存在的等量关系(不写理由).

(1)如图(1),请直接写出∠A,∠P,∠C之间存在的等量关系(不写理由);
(2)如图(2),写出∠A,∠P,∠C之间存在的等量关系,并说明理由;
(3)如图(3),请直接写出∠A,∠P,∠C之间存在的等量关系(不写理由).
考点:平行线的性质
专题:
分析:(1)过点P作PE∥AB,然后根据两直线平行,同旁内角互补解答;
(2)过点P作PE∥AB,根据两直线平行,内错角相等可得∠A=∠APE,∠C=∠CPE,再根据∠APC=∠APE+∠CPE等量代换即可得解;
(3)过点P作PE∥AB,然后根据两直线平行,同旁内角互补解答.
(2)过点P作PE∥AB,根据两直线平行,内错角相等可得∠A=∠APE,∠C=∠CPE,再根据∠APC=∠APE+∠CPE等量代换即可得解;
(3)过点P作PE∥AB,然后根据两直线平行,同旁内角互补解答.
解答: 解:(1)∠A+∠C+∠P=360°;
解:(1)∠A+∠C+∠P=360°;
(2)∠A+∠C=∠P.
证明如下:过点P作PE∥AB,
∵AB∥CD,
∴PE∥CD(平行于同一条直线的两条直线平行),
∴∠A=∠APE,∠C=∠CPE(两直线平行,内错角相等),
∵∠APC=∠APE+∠CPE,
∴∠APC=∠A+∠C;
(3)∠P=∠C-∠A.
 解:(1)∠A+∠C+∠P=360°;
解:(1)∠A+∠C+∠P=360°;(2)∠A+∠C=∠P.
证明如下:过点P作PE∥AB,
∵AB∥CD,
∴PE∥CD(平行于同一条直线的两条直线平行),
∴∠A=∠APE,∠C=∠CPE(两直线平行,内错角相等),
∵∠APC=∠APE+∠CPE,
∴∠APC=∠A+∠C;
(3)∠P=∠C-∠A.
点评:本题考查了平行线的性质,此类题目,过拐点作平行线是解题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
 如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F.
如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F. 已知y是x的反比例函数,且当x=4,y=-1.
已知y是x的反比例函数,且当x=4,y=-1. 如图,AB是⊙O的直径,AC是弦,OD⊥AC于点E,交⊙O于点F,连接BF、CF,∠D=∠BFC.
如图,AB是⊙O的直径,AC是弦,OD⊥AC于点E,交⊙O于点F,连接BF、CF,∠D=∠BFC.
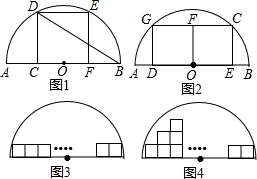 正方形和圆都是人们比较喜欢的图形,给人以美得感受.我校数学兴趣小组在研究性学习中发现:
正方形和圆都是人们比较喜欢的图形,给人以美得感受.我校数学兴趣小组在研究性学习中发现: 为了解我市某学校“书香校园”的建设情况,检查组在该校随机抽取40名学生,调查了解他们一周阅读课外书籍的时间,并将调查结果绘制成如图的频数直方图(每小组的时间值包含最小值,不包含最大值),根据图中信息估计该校学生一周课外阅读时间不少于4小时的人数占全校人数的百分数约等于
为了解我市某学校“书香校园”的建设情况,检查组在该校随机抽取40名学生,调查了解他们一周阅读课外书籍的时间,并将调查结果绘制成如图的频数直方图(每小组的时间值包含最小值,不包含最大值),根据图中信息估计该校学生一周课外阅读时间不少于4小时的人数占全校人数的百分数约等于