题目内容
 如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F.
如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F.(1)若AB=4,BC=6,求EC的长;
(2)若∠F=55°,求∠BAE和∠D的度数.
考点:平行四边形的性质
专题:
分析:(1)利用平行四边形的性质以及平行线的性质得出∠2=∠3,进而得出AB=BE即可得出答案;
(2)利用平行线的性质以及三角形内角和定理得出即可.
(2)利用平行线的性质以及三角形内角和定理得出即可.
解答: 解:(1)∵四边形ABCD是平行四边形,
解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,∴∠1=∠2,
又∵∠1=∠3,
∴∠2=∠3,
∴AB=BE=4,
∴EC=BC-BE=6-4=2;
(2)∵AB∥CD,
∴∠3=∠F=55°,
∴∠1=∠3=55°,
在△ADF中,∠D=180°-∠1-∠F=70°.
 解:(1)∵四边形ABCD是平行四边形,
解:(1)∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,∴∠1=∠2,
又∵∠1=∠3,
∴∠2=∠3,
∴AB=BE=4,
∴EC=BC-BE=6-4=2;
(2)∵AB∥CD,
∴∠3=∠F=55°,
∴∠1=∠3=55°,
在△ADF中,∠D=180°-∠1-∠F=70°.
点评:此题主要考查了平行四边形的性质以及平行线的性质等知识,熟练应用平行四边形的性质得出是解题关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 甲、乙、丙、丁4个人步行的距离和花费的时间如图,按平均值计算,则走的最慢的是( )
甲、乙、丙、丁4个人步行的距离和花费的时间如图,按平均值计算,则走的最慢的是( )| A、甲 | B、乙 | C、丙 | D、丁 |
若代数式(x+a)(x-
)的结果中不含字母x的一次项,那么a的值是( )
| 1 |
| 2 |
| A、0 | ||
| B、2 | ||
C、
| ||
D、-
|
 如图,已知EF∥AD,∠1=∠2,∠BAC=68°,求∠AGD的度数.
如图,已知EF∥AD,∠1=∠2,∠BAC=68°,求∠AGD的度数.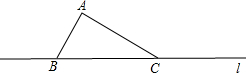 已知:如图,点A是直线l外一点,B,C两点在直线l上,∠BAC=90°.
已知:如图,点A是直线l外一点,B,C两点在直线l上,∠BAC=90°.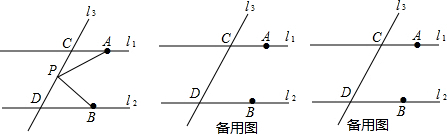
 一列快车从甲地匀速驶乙地,一列慢车从乙地匀速驶往甲地,慢车先发车半小时.设先发车辆行驶的时间为x/h,两车之间的距离为y/km,图中的折线表示y与x之间的函数关系,根据图象解决以下问题:
一列快车从甲地匀速驶乙地,一列慢车从乙地匀速驶往甲地,慢车先发车半小时.设先发车辆行驶的时间为x/h,两车之间的距离为y/km,图中的折线表示y与x之间的函数关系,根据图象解决以下问题: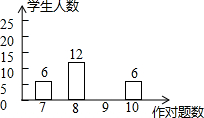 数学老师布置10道选择题当堂测试,统计结果每人至少答对7道题,数学课代表对全班48名同学的答题情况绘制了条形统计图.
数学老师布置10道选择题当堂测试,统计结果每人至少答对7道题,数学课代表对全班48名同学的答题情况绘制了条形统计图.