题目内容
 已知y是x的反比例函数,且当x=4,y=-1.
已知y是x的反比例函数,且当x=4,y=-1.(1)函数y与x之间的函数表达式为
(2)画出函数的图象,并根据图象直接写出当一3≤x≤-
| 1 |
| 2 |
(3)若点P(x1,y1)、Q(x2,y2)在函数的图象上,且x1<x2,试比较y1与y2的大小.
考点:待定系数法求反比例函数解析式,反比例函数的图象,反比例函数图象上点的坐标特征
专题:
分析:(1)利用待定系数法确定反比例函数的解析式即可;
(2)根据自变量的取值范围确定图象的位置,根据图象的变化发现增减性,从而确定取值范围;
(3)根据两个自变量的取值不同确定函数值的大小即可.
(2)根据自变量的取值范围确定图象的位置,根据图象的变化发现增减性,从而确定取值范围;
(3)根据两个自变量的取值不同确定函数值的大小即可.
解答:解:(1)设反比例函数的解析式为y=
,
∵当x=4,y=-1,
∴k=xy=-4,
∴函数关系式为y=-
;
(2)函数图象为:

由图象知:当一3≤x≤-
时,y的取值范围
≤y≤8;
(3)当x1<x2<0时y1<y2,当x1<0<x2时y1>y2,
当0<x1<x2时y1<y2.
| k |
| x |
∵当x=4,y=-1,
∴k=xy=-4,
∴函数关系式为y=-
| 4 |
| x |
(2)函数图象为:

由图象知:当一3≤x≤-
| 1 |
| 2 |
| 8 |
| 3 |
(3)当x1<x2<0时y1<y2,当x1<0<x2时y1>y2,
当0<x1<x2时y1<y2.
点评:本题考查了反比例函数的有关知识,解题的关键是确定反比例函数的解析式,然后正确的作出反比例函数的图象,难度不大.

练习册系列答案
相关题目
 如图,已知EF∥AD,∠1=∠2,∠BAC=68°,求∠AGD的度数.
如图,已知EF∥AD,∠1=∠2,∠BAC=68°,求∠AGD的度数.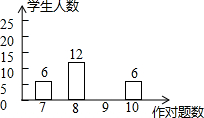 数学老师布置10道选择题当堂测试,统计结果每人至少答对7道题,数学课代表对全班48名同学的答题情况绘制了条形统计图.
数学老师布置10道选择题当堂测试,统计结果每人至少答对7道题,数学课代表对全班48名同学的答题情况绘制了条形统计图.
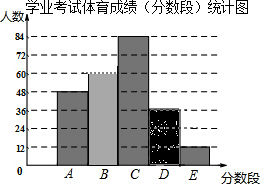 为了了解我市初四学生学业考试体育成绩,现从全市该年级学生中随机抽取了240名学生的体育成绩进行统计分段(A:100~90分;B:90~80分;C:80~70分;D:70~60分;E:60分以下)后,作出了频数分布直方图的一部分(每组数据含最大值,不含最小值).请根据频数分布直方图,解答下列问题:
为了了解我市初四学生学业考试体育成绩,现从全市该年级学生中随机抽取了240名学生的体育成绩进行统计分段(A:100~90分;B:90~80分;C:80~70分;D:70~60分;E:60分以下)后,作出了频数分布直方图的一部分(每组数据含最大值,不含最小值).请根据频数分布直方图,解答下列问题: 已知:如图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,∠B-∠D=24°,求∠GEF的度数.
已知:如图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,∠B-∠D=24°,求∠GEF的度数.
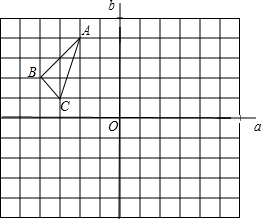 在一个网格图中有一个△ABC,直线a,b相交于点O,(不留作图痕迹但请标记出对应点的字母)
在一个网格图中有一个△ABC,直线a,b相交于点O,(不留作图痕迹但请标记出对应点的字母)