题目内容
已知直线l1∥l2,l3和l1,l2分别交于C,D两点,点A,B分别在线l1,l2上,且位于l3的左侧,点P在直线l3上,且不和点C,D重合.
(1)如图1,有一动点P在线段CD之间运动时,试确定∠1、∠2、∠3之间的关系,并给出证明;
(2)如图2,当动点P线段CD之外运动时,上述的结论是否成立?若不成立,并给出证明.

(1)如图1,有一动点P在线段CD之间运动时,试确定∠1、∠2、∠3之间的关系,并给出证明;
(2)如图2,当动点P线段CD之外运动时,上述的结论是否成立?若不成立,并给出证明.

考点:平行线的性质
专题:
分析:(1)过点P作PE∥l1,根据l1∥l2可知PE∥l2,故可得出∠1=∠APE,∠3=∠BPE.再由∠2=∠APE+∠BPE即可得出结论;
(2)设PB与l1交于点F,根据l1∥l2可知∠3=∠PFC. 在△APF中,根据∠PFC是△APF的一个外角即可得出结论.
(2)设PB与l1交于点F,根据l1∥l2可知∠3=∠PFC. 在△APF中,根据∠PFC是△APF的一个外角即可得出结论.
解答: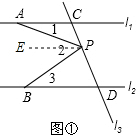 (1)∠2=∠1+∠3.
(1)∠2=∠1+∠3.
证明:如图②,过点P作PE∥l1,
∵l1∥l2,
∴PE∥l2,
∴∠1=∠APE,∠3=∠BPE.
又∵∠2=∠APE+∠BPE,
∴∠2=∠1+∠3;

(2)上述结论不成立,新的结论:∠3=∠1+∠2.
证明:如图①,设PB与l1交于点F,
∵l1∥l2,
∴∠3=∠PFC.
在△APF中,
∵∠PFC是△APF的一个外角,
∴∠PFC=∠1+∠2,即∠3=∠1+∠2.
 (1)∠2=∠1+∠3.
(1)∠2=∠1+∠3.证明:如图②,过点P作PE∥l1,
∵l1∥l2,
∴PE∥l2,
∴∠1=∠APE,∠3=∠BPE.
又∵∠2=∠APE+∠BPE,
∴∠2=∠1+∠3;

(2)上述结论不成立,新的结论:∠3=∠1+∠2.
证明:如图①,设PB与l1交于点F,
∵l1∥l2,
∴∠3=∠PFC.
在△APF中,
∵∠PFC是△APF的一个外角,
∴∠PFC=∠1+∠2,即∠3=∠1+∠2.
点评:本题考查的是平行线的性质,根据题意作出辅助线,构造出平行线是解答此题的关键.

练习册系列答案
相关题目
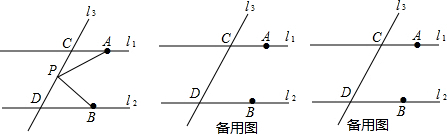

 已知:如图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,∠B-∠D=24°,求∠GEF的度数.
已知:如图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,∠B-∠D=24°,求∠GEF的度数.

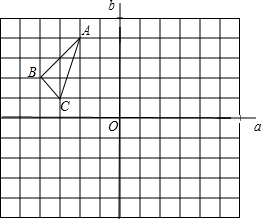 在一个网格图中有一个△ABC,直线a,b相交于点O,(不留作图痕迹但请标记出对应点的字母)
在一个网格图中有一个△ABC,直线a,b相交于点O,(不留作图痕迹但请标记出对应点的字母) 已知等腰△ABC中,AB=AC,一腰上的中线BD把这个△ABC的周长分成15cm和6cm两部分,求这个等腰三角形的各边长?(提示:用方程思想解决)
已知等腰△ABC中,AB=AC,一腰上的中线BD把这个△ABC的周长分成15cm和6cm两部分,求这个等腰三角形的各边长?(提示:用方程思想解决)