题目内容
 如图,AB是⊙O的直径,AC是弦,OD⊥AC于点E,交⊙O于点F,连接BF、CF,∠D=∠BFC.
如图,AB是⊙O的直径,AC是弦,OD⊥AC于点E,交⊙O于点F,连接BF、CF,∠D=∠BFC.(1)求证:AD是⊙O的切线;
(2)若AC=8,EF=2.
①求⊙O的半径;
②设AD=x,FD=y,求x,y的值.
考点:切线的判定,勾股定理
专题:
分析:(1)由OD⊥AC,∠D=∠BFC与圆周角定理,易求得∠EAD+∠BAC=90°,即可证得AD是⊙O的切线;
(2)①利用垂径定理得到EC=
AC;然后在直角△OEA中,利用勾股定理来求FC的长度即可;
②在Rt△OAD和Rt△AED中,利用勾股定理列出关于x、y的方程,联立方程组,解方程组即可.
(2)①利用垂径定理得到EC=
| 1 |
| 2 |
②在Rt△OAD和Rt△AED中,利用勾股定理列出关于x、y的方程,联立方程组,解方程组即可.
解答:(1)证明:∵OD⊥AC,
∴∠AED=90°,
∴∠EAD+∠D=90°,
∵∠D=∠BFC,∠BFC=∠BAC,
∴∠BAC=∠D,
∴∠EAD+∠BAC=90°,
即OA⊥AD,
∴AD是⊙O的切线;
(2)①设⊙O的半径为r.
∵AC是弦,OD⊥AC于点E,AC=8,
∴EC=
AC=4,
∴在直角△OEA中,由勾股定理得到:r2=(r-2)2=42,
解得 r=5.
即⊙O的半径是5;
②在Rt△OAD和Rt△AED中得到:
,
解得
.
∴∠AED=90°,
∴∠EAD+∠D=90°,
∵∠D=∠BFC,∠BFC=∠BAC,
∴∠BAC=∠D,
∴∠EAD+∠BAC=90°,
即OA⊥AD,
∴AD是⊙O的切线;
(2)①设⊙O的半径为r.
∵AC是弦,OD⊥AC于点E,AC=8,
∴EC=
| 1 |
| 2 |
∴在直角△OEA中,由勾股定理得到:r2=(r-2)2=42,
解得 r=5.
即⊙O的半径是5;
②在Rt△OAD和Rt△AED中得到:
|
解得
|
点评:此题考查了切线的判定、圆周角定理以及勾股定理的应用.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
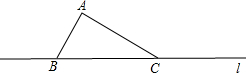 已知:如图,点A是直线l外一点,B,C两点在直线l上,∠BAC=90°.
已知:如图,点A是直线l外一点,B,C两点在直线l上,∠BAC=90°.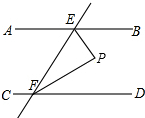 请将下列证明过程补充完整:
请将下列证明过程补充完整: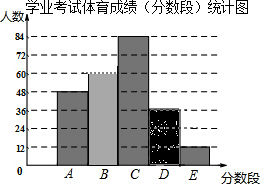 为了了解我市初四学生学业考试体育成绩,现从全市该年级学生中随机抽取了240名学生的体育成绩进行统计分段(A:100~90分;B:90~80分;C:80~70分;D:70~60分;E:60分以下)后,作出了频数分布直方图的一部分(每组数据含最大值,不含最小值).请根据频数分布直方图,解答下列问题:
为了了解我市初四学生学业考试体育成绩,现从全市该年级学生中随机抽取了240名学生的体育成绩进行统计分段(A:100~90分;B:90~80分;C:80~70分;D:70~60分;E:60分以下)后,作出了频数分布直方图的一部分(每组数据含最大值,不含最小值).请根据频数分布直方图,解答下列问题:

 如图,AE,AD分别是△ABC的高和角平分线,且∠B=30°,∠C=70°.
如图,AE,AD分别是△ABC的高和角平分线,且∠B=30°,∠C=70°.